導関数の公式と求め方がひと目でわかる！練習問題付き♪

微分は平面図形などと違い、頭の中でイメージしにくい分野の一つです。

なので、苦手意識を持っている人も多いです。

しかし、微分は早稲田大学や慶應大学などの難関大学ではもちろんのこと、他大学でも毎年出題されていると言ってもよいです。

（2014年度の早稲田大学の入試では、文理問わずほぼすべての学部で出題されています。）

それくらい、微分は入試にとって重要な分野なのです。

今回は微分とは何か？についてや微分の基礎について数学が苦手な文系学生にも分かり易く、簡単にまとめました。是非読んでみて下さい！

【PR】勉強を効率的に継続して、志望校に合格したい方必見！

↓無料ダウンロードはこちら↓

 

１．導関数

１－１.  導関数とは？

導関数について分かり易く解説していきます。例えば、y=f(x)という関数があったとします。この関数を微分すると、f´(x)という関数が得られますよね。このf´(x)が導関数なのです！

つまり、一言でまとめると、「導関数とは、ある関数を微分して得られた新たな関数」ということです。簡単ですよね！?

従って、問題で、「関数y=f(x)の導関数を求めよ」という問題が出たとすると、y=f(x)を微分すればいいということになります。(f´(x)の求め方については、上記の「２.微分係数」を参考にしてください。aの箇所をxに変更すれば良いだけです。)

 

１－２.  導関数の楽な求め方

しかし、導関数を求めるとき（微分するとき）に、毎回毎回定義に従って求めるのは非常に面倒ですよね。ここでは、そんな手間を省くための方法を紹介していきます！下のイラストをご覧ください。

 

 

２．微分の定義の確認

２－１．平均変化率、微分するとは？

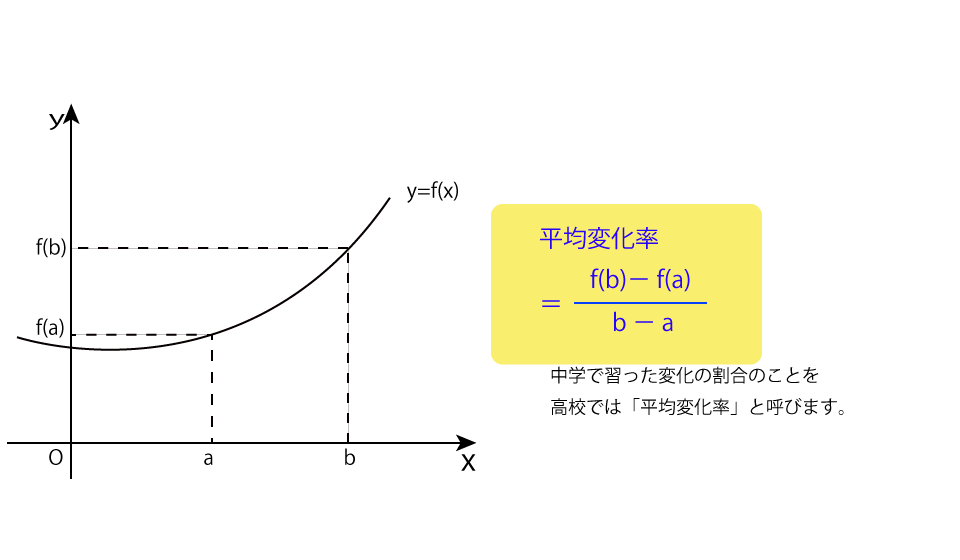
平均変化率…　これは意外なことにみなさんは既に中学生のときに学習しています。（変化の割合という言葉で習ったかもしれません）まずはこれのおさらいから入ります。 中学校で関数を学習したときに、「直線の傾きを求める」という問題をみなさん一度は解いたことがあると思います。そうです！これがまさに平均変化率（変化の割合）なのです！ 下の図で復習しましょう！

このことを高校では平均変化率と呼んでいます。これを、y=f(x)という関数をもとに考えると、下の図のようになりますね。

平均変化率についての理解はそこまで難しくはなかったと思います。 ではここで、平均変化率の式において、aをとある数とし、bをaに限りなく近づけるとどうなるでしょうか？「限りなく近づける」ということは、決してb=aにはなりませんよね。

したがって分母は０にはならないので、この平均変化率の式はなんらかの値になります。そのなんらかの値を「f´(a)」と名付けるのが、微分の世界なのです。

つまり、y=f(x)を微分するとは、「y=f(x)のとあるＸ座標a(固定)において、Ｘ座標上を動くbが限りなくaに近づいたときのf(x)の値を求めること」と言えます。（この値はf´(a)と表されます。）

 

２－２．微分係数

先ほどで、なんらかの値f´(a)についての説明を行いました。そのf´(a)を、関数y=f(x)のx=aにおける微分係数、または変化率と呼んでいます。

つまり、「f´(a)はy=f(x)のx=aにおける微分係数です。」といった使い方をします。 ではここで、関数f(x)のx=aにおける微分係数（つまり、f´(a)のこと）の定義を紹介します。 特に、右側の式はよく使うことが多いので、しっかり頭に入れておきましょう。

 

３．  練習問題

いかがでしたでしょうか？ここまでで学習してきたことは微分の超基礎的な内容なので、必ずマスターしてくださいネ！ ここからは練習問題で微分の基礎を定着させていきましょう！（もちろん解説付きです）

以下が解答＆解説です。ご確認ください！

 

導関数のまとめ

いかがでしたでしょうか。微分は難易度が高い問題も多く、計算量が多いのも事実です。ですので、ここでしっかりと基礎を固めて、単純なミスをしないようにしていきましょう。

この記事の執筆者

ニックネーム：やっすん

早稲田大学商学部4年
得意科目：数学