【必ず解けるようにしておきたい因数分解の問題】高校数学の頻出分野を基礎から解説！

因数分解の問題をいくつか出題します。

因数分解は数学において非常に重要な分野の１つです。因数分解は問題をたくさん解くことで力が付きます。

本記事で様々な因数分解の問題を解いて力をつけましょう！

もちろん解答＆解説もあるので、安心して解いてください！

※因数分解のやり方・公式を見直したい人は、因数分解について解説した記事をご覧ください。

→因数分解に役立つ記事まとめはコチラ！

 

1：因数分解の問題（たすき掛け）

まずはたすき掛けを使って解く因数分解の問題をいくつか解いていきましょう！

問題１

x²+12x+35

を因数分解せよ。

解答＆解説

まず、xの係数12と定数項35に注目します。

掛け算すれば35、足し算すれば12になる２つの数字を探せば良いのでした。

つまり、5と7の組み合わせですね。

よって答えは、

(x+5)(x+7)・・・（答）

となります。

 

問題２

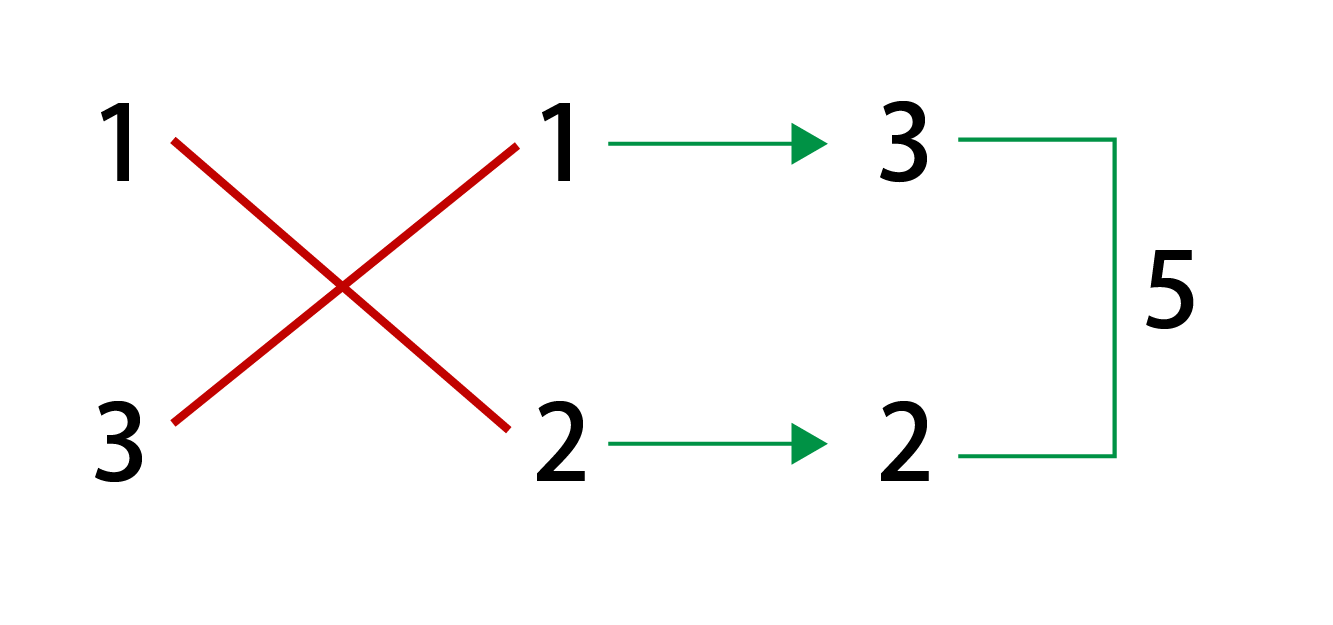
3x²+5x+2

を因数分解せよ。

解答＆解説

たすき掛けを行うと、以下のようになりますね。

したがって、

(x+1)(3x+2)・・・（答）

となります。

 

2：因数分解の問題（公式）

次は、因数分解の公式を使う問題を解いてみましょう！

※因数分解の公式を再確認したい人は、因数分解の公式を紹介した記事をご覧ください。

問題１

x²-8x+16

を因数分解せよ。

解答＆解説

これは２乗の因数分解の公式

x²-2ax+a²=(x-a)²

を使えば良いですね。

よって答えは

(x-4)²・・・（答）

となります。

 

問題２

8x³+12x²y+6xy²+y³

を因数分解せよ。

解答＆解説

これは３乗の公式

(a+b)³=a³+3a²y+3ab²+b³

を使えば良いですね。

よって、

(2x+y)³・・・（答）

となります。

 

3：因数分解の問題（置き換え）

次は置き換えを使った問題を解いてみましょう！

問題１

x³+2x+x²+2

を因数分解せよ

解答＆解説

まずはx³+2xをxでくくってみましょう。

x(x²+2)+(x²+2)

となりますね。ここで、(x²+2)という塊ができたので、

(x²+2) = Aと置き換えてみましょう。すると、

xA + A

となるので、Aでくくって、

A(x+1)

が得られます。ここで、A=(x²+2)なので、

(x²+2)(x+1)・・・（答）

となります。

 

問題２

(5x+6)²+8(5x+6)+15

を因数分解せよ。

解答＆解説

(5x+6)を塊とみましょう。

(5x+6)=Aと置き換えると、

A²+8A+15

= (A+3)(A+5)

となるので、Aを元に戻して

(5x+9)(5x+11)・・・（答）

となります。

 

さいごに

因数分解の問題をいくつか紹介しました。

因数分解はたくさんの問題を解くことで力がつきます。

ぜひ学校で配布された問題集などでたくさんの問題を解いてください！

→因数分解に役立つ記事まとめはコチラ！

この記事の執筆者

ニックネーム：やっすん

早稲田大学商学部4年
得意科目：数学