【三角関数の基礎】必ず覚えておかなくてはならない５つの性質とは？

三角関数は、大学受験に出題されやすい範囲の一つです。

近年では、2014年慶應商学部、2015年早稲田社会科学部、人間科学部、国際教養学部などで出題されています。

その他の多くの大学でも、少なくとも5年に一度は出題されているくらい頻度が高いです。

三角関数は、考え方が重要で、特に定義や性質をしっかりとマスターする必要があります。

今回は、最もベーシックとなる定義と５つの性質をまとめました。是非、この機会に三角関数をマスターしましょう。

三角関数の基本的な理解に役立つ記事のまとめもぜひ参考にしてみてください！

 

 

 

1. 三角関数の定義

三角関数は数Ⅰと数Ⅱで定義は違っていますが、本質は一緒です。

数Ⅰバージョン(三角比）

数Ⅰでは、誰でもが直感的に理解出来るように、三角関数が簡易的な定義になっています。

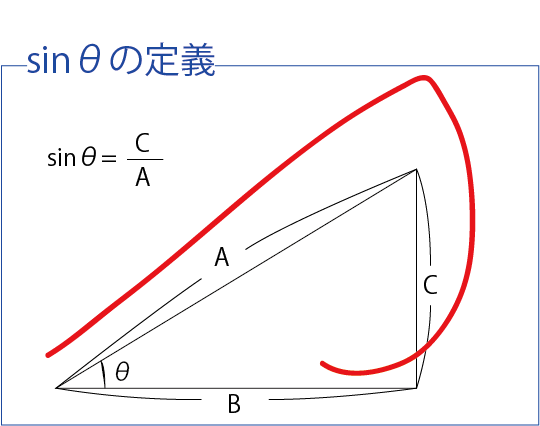
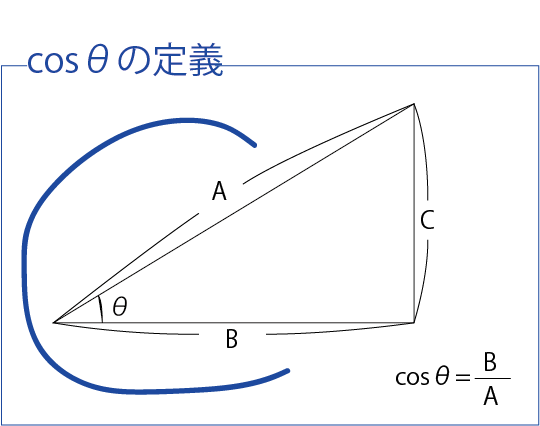
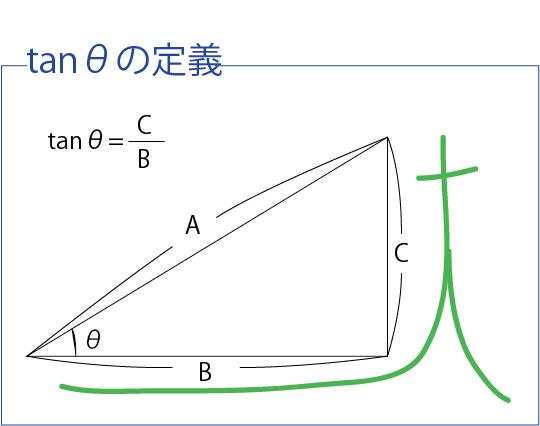
筆記体の書き順で何が分母で何が分子にくるかが分かります。

先に通る方：分母⇒後に通る方：分子

Sを書くのにA→Cに向かいます。

Cを書くのにA→Bに向かいます。

 

Tを書くのにB→Cに向かいます。

※sin、cos、tanについてもっと深く学習したい人は、sin・cos・tanについて詳しく解説した記事をご覧ください。

 

覚えかた付きですごく分かりやすいのですが一つ問題があります。

それは、θ≧180°の時に定義出来ないという点です。それを数Ⅱで解決してくれます。

 

数Ⅱバージョン

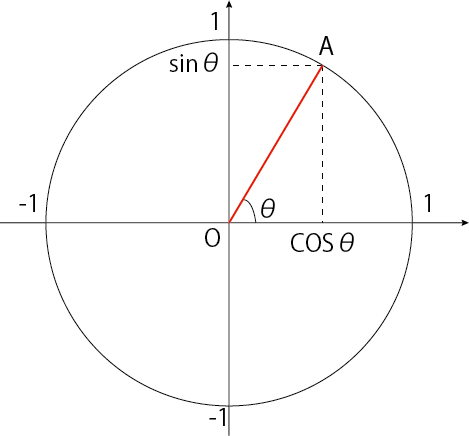
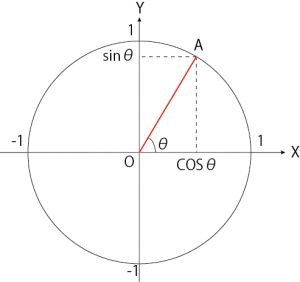
数Ⅱでは、円を用いて定義します。

今回は、簡単に理解しやすいように半径が１の単位円を使って定義します。

 

単位円以外の半径Rの円では

tanθは傾きを表します。

 

「cosθってなんだ？」と漠然と疑問に思う事があると思います。そんな時に、頭の中に単位円を思い出し、そのX座標の事であると思い出すと問題を解く上で、考えやすくなります。

しっかり覚えましょう。

 

2. 三角関数の必ず覚えなくてはならない5つの性質

①sin^２θ+cos^２θ=1

②

①、②とも三角関数の定義の単位円を思い出せば、簡単です。

①は単位円の方程式がX^２+Y^２=1だから、それにX=cosθ、Y=sinθを代入すれば出来ます。

また、②はだからX=cosθ、Y=sinθを代入すれば完成です。

※以上の公式をもっと深く学習したい人は、sin²θ+cos²θ=1について詳しく解説した記事をご覧ください。

 

③

これは、①のsin^２θ+cos^２θ=1をcos^２θで割るだけです。

②より成立します。

 

④三角関数グラフ

しつこいようですが、もう一度思い出していただきたいのが、こちらの定義です。　tanθ：傾き

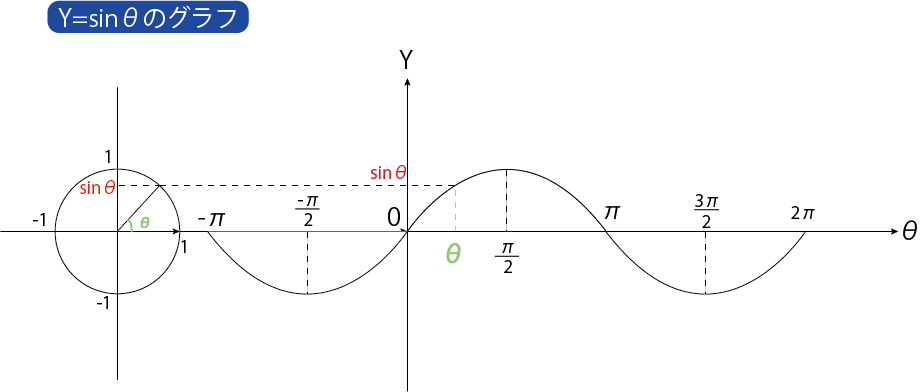
単位円のY座標は、sinθを表します。

だからグラフは、単位円を回転する事なく、グラフにそのままプロットします。

sinθのとりうる範囲は-1≦Y≦1です。

 

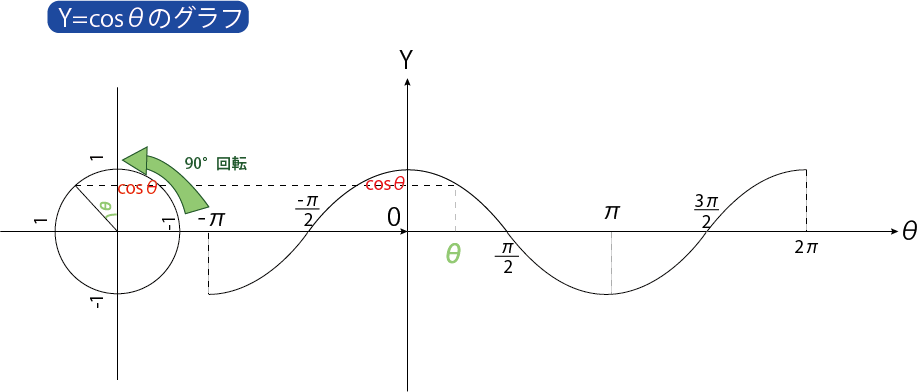
単位円のX座標は、cosθを表します。

だから、単位円のX座標を90°回転させなくてはなりません。回転後は、それをプロットしていけば良いです。

cosθのとりうる範囲は-1≦Y≦1になります。

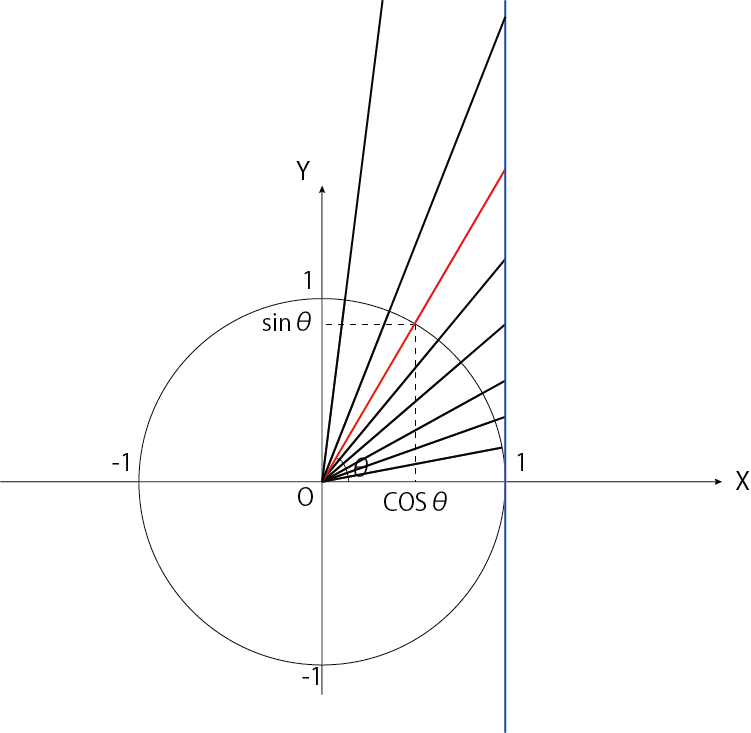
最後は、Y=tanθのグラフです。

　tanθ：傾き

下図を見ると、傾きが徐々に大きくなっていくのが分かりますね。

 

グラフに表すと以下になります。

上のグラフを見ていただければ分かりますが、

の時（赤線の時）は、Y=無限大になってしまいます。

だから、範囲は

で、Yはすべての実数値をとります。

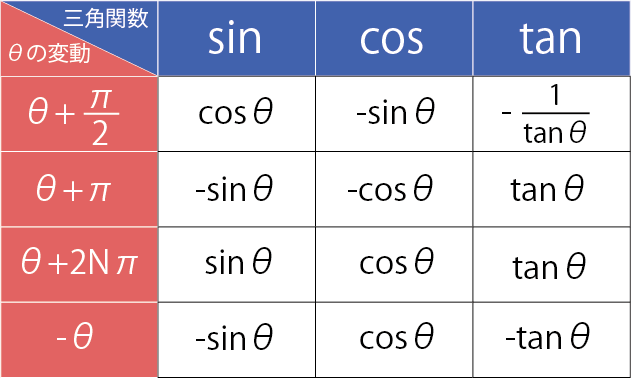
⑤三角関数　θによる変動

この表はかなり重要です。

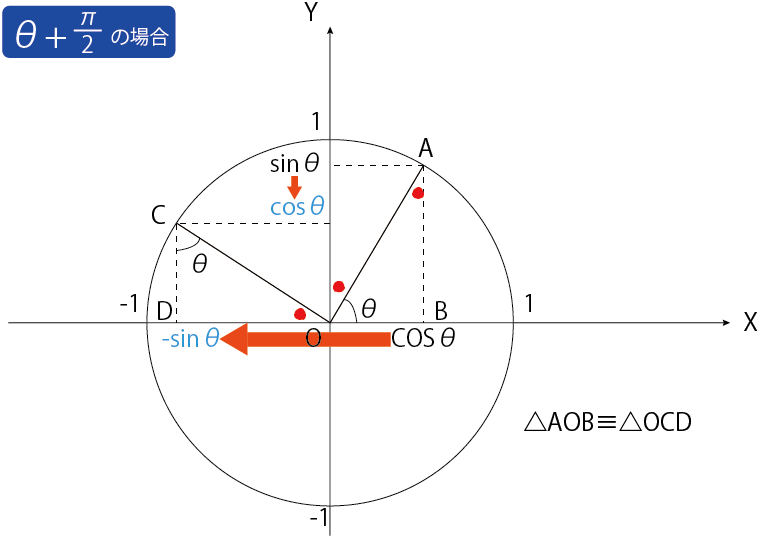
これもコツは頭の中で

を思い浮かべ、回転させてみる事です！

実際に書いてみると、一目瞭然ですね。

一つの辺と、２つの角度の大きさが等しいので、△AOB≡△OCDになります。あとは、合同条件よりAB=OD=sinθ、OB=CD=cosθになるので、sinθ⇒cosθ、cosθ⇒-sinθになります。

 

表の中の、値は上記のように解けば、証明出来ます。是非やってみてください。

忘れた時は、このように書いて、思い出すことができますが、基本は頭の中で、どのように変換出来るかを瞬時に導ける事が大事です。

しっかりと練習を積んでください！

この記事の執筆者

ニックネーム：受験のミカタ編集部

「受験のミカタ」は、難関大学在学中の大学生ライターが中心となり運営している「受験応援メディア」です。