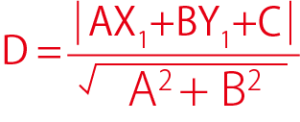【点と直線の距離の公式の覚え方】証明の方法や練習問題も解説！

点と直線の距離は、まずは公式をしっかりと覚えましょう！

また、点と直線の距離の証明は、数学的に大事な要素が含まれているので、合わせて覚えてしまいましょう。今回の記事はすごく簡単に証明出来る「三角形の相似」を使った方法で証明します。

最後に、試験などでよく出る、定番の問題も出題しましたので解いてみてください！

 

1. 点と直線の距離　定義

 

 

2. 点と直線の距離　公式

点(X1,Y1)と直線AX+BY+C=0の距離Dは

になります。頭に叩き込みましょう。

 

3. 点と直線の距離　公式　証明

点と直線の距離の証明は少し難しいですが、三角形の相似を使えば、比較的楽に証明出来るので、今回はその方法を紹介します。

 

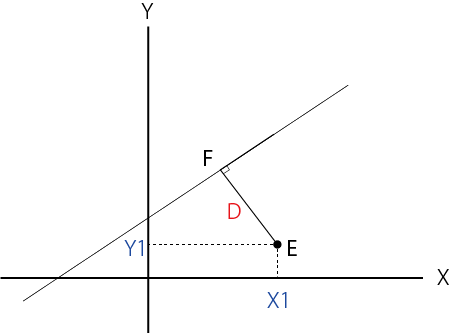
点E(X1,Y1)と直線l(AX+BY+C=0)の距離が、最終的に

になればよいです。

B≠0の時

AX+BY+C=0は分かりずらいので

という形に変形します。

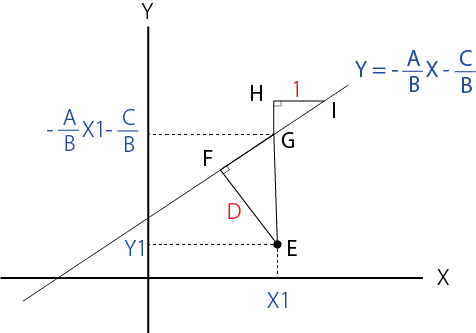
直線l上のX=X1の点をG、X=X1+1の点をIとします。また、EGの延長戦とIをX軸に平行に引いた線の交点をHとします。(下図の通り）

 

 

△EFGと△IHGは三つの角度が等しいので、相似であることが分かります。

だから

EG:EF=IG:IHが成り立ちます。

あとは、この比を解いていくだけです。

これは、Y1が直線lより、上にある可能性もあるので、正負の判別がつきません。だから絶対値をつけなくてはいけません。

三平方の定理より

よって

あとは、この式を解いていくだけです。

計算の過程は省略します！是非、解いてみて答えが

になることを確かめてください。

B=0の時

B=0なので、直線lはAX1+C=0⇔

よって

これはB=0の時の

にあてはまるので、B=0のときも成り立ちます。

以上が、点と直線の距離の証明です。

 

4. 点と直線の距離　問題

点と直線の距離の問題を早速解いていきましょう。

【問題】

 

【解答】

これは、一見、直線と曲線の距離なので、『点と直線の距離』を使わないのではないか？と思うかもしれません。

しかし、これは典型的な『点と直線の距離』の問題です。

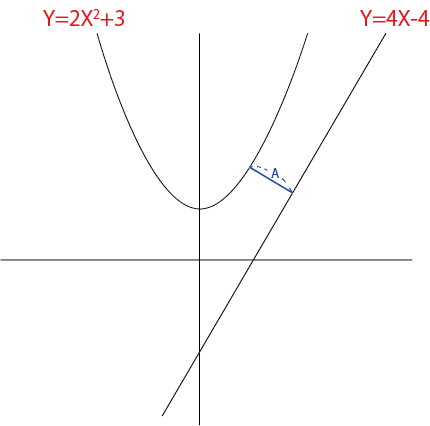
まず、直線Y=2X^２+3上の点を(a、2a^２+3)とします。

この点とY=4X-4の距離を求めます。

また、Y=4X-4は変形すると4X-Y-4=0になります。

あとは、点と直線の距離を使います。

A

=|4a-(2a²+3)-4| / √(1²+4²)

=|-2(a-1)²-5| / √17

よってa=1のときAは最小になるので代入すると

A=5/√17・・・（答）

となります。

 

 

点と直線の距離のまとめ

いかがでしたか？

解けなかった方は時間がたった後にもう一度復習してみてください！

がんばれ受験生！

 

この記事の執筆者

ニックネーム：受験のミカタ編集部

「受験のミカタ」は、難関大学在学中の大学生ライターが中心となり運営している「受験応援メディア」です。