受験のミカタでは、Cookieを使用してサービスを提供しています。当サイトにアクセスすることにより、プライバシーポリシーに記載されているCookieの使用に同意したものとします。

定期テスト前必見！三角関数の合成の公式や証明をわかりやすく解説！

数学 2022.12.26

定期テスト前必見！三角関数の合成の公式や証明をわかりやすく解説！

三角関数の中でも、最大値、最小値を求める問題が多く、2015年度の早稲田大学の入試では、人間科学部と国際教養学部で問題が出題されました。

そのうち、人間科学部では相加相乗平均で解答する問題だったのに対して、国際教養学部では、典型的な三角関数の合成を利用して解答する問題でした。

その他、多くの大学でも三角関数の最大値、最小値を求める問題が出題されています。

勉強の進んでいる受験生なら合成の公式が分かるのは当たり前ですが、最大・最小問題を見た時に合成を使えるようになれるかどうかが受験では大事です。

今回は三角関数の合成の公式や証明だけでなく、合成をするときのコツを紹介します。

三角関数の証明の理解に役立つ記事のまとめもぜひ参考にしてみてください！

【PR】勉強を効率的に継続して、志望校に合格したい方必見！

スタキャスバナー

↓無料ダウンロードはこちら↓

GooglePlayStoreのボタン

appleStoreのボタン

【目次】

三角関数の合成（公式）

三角関数の合成（証明）

三角関数の合成（練習問題）

三角関数の合成（解き方のコツ）

①方程式、不等式を解く場合

②最小値、最大値を求める場合

1. 三角関数の合成（公式）

三角関数の合成は、以下の式をしっかり覚えましょう。

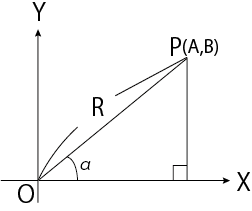
2. 三角関数の合成（証明）

三角関数の合成を証明する。

三平方の定理より

$R=\sqrt {A^2+B^2}$

また、三角関数の定義より

$cos \alpha=\frac{A}{R}$ ⇔A=Rcosα

$sin \alpha=\frac{B}{R}$ ⇔B=Rsinα

以上を使って

Asinθ+Bcosθを展開していく。

Asinθ+Bcosθ=Rcosαsinθ+Rsinαcosθ=R(cosαsinθ+sinαcosθ)

加法定理より

R(cosαsinθ+sinαcosθ)=Rsin(θ+α)= $\sqrt {A^2+B^2}sin(\theta+\alpha)$

この時のαは $cos \alpha=\frac{A}{R}$ , $sin \alpha=\frac{B}{R}$ から

$cos \alpha=\frac{A}{\sqrt {A^2+B^2}}$

$sin \alpha=\frac{B}{\sqrt {A^2+B^2}}$

を満たす角度になる。

参考：加法定理証明・簡単な覚え方・語呂合わせ

3. 三角関数の合成（練習問題）

sinθ+cosθに合成を行うとどのようになるかやってみる。

$sin \theta+cos \theta=\sqrt2 sin (\theta+\alpha)$

この時、αは・・・

$sin \alpha=\frac{1}{\sqrt2}$
$cos \alpha=\frac{1}{\sqrt2}$

を満たすαなので

$\alpha=\frac{\pi}{4}$ (基本的には0≦α≦2πのものを使う。)

よって

$sin \theta+cos \theta=\sqrt2 sin (\theta+\frac{\pi}{4})$

になる。

4. 三角関数の合成（解き方のコツ）

どのような時に、合成関数を使うのかが分からない人が多いと思います。しかし、多くの問題を見ていると、合成関数を使うのは以下の２つの場面が多いです。

①方程式、不等式を解く場合

②最小値、最大値を求める場合（こちらが圧倒的に多いです。）

理由は

三角関数を合成する事で、今までsinとcosを同時に使っていた方程式をsinのみの方程式に変換出来るからです。つまり変数を一つにする事で、関数の動向が見やすくなります。だから、最小値、最大値を求めやすくなります。

それぞれの問題をといていきましょう。

①方程式、不等式を解く場合

$\sqrt 3cos\theta - sin\theta=0$

三角関数の合成を使って・・

$2sin(\theta+\alpha)=0$

この時

$sin \alpha=\frac{\sqrt 3}{2}$

$cos \alpha=-\frac{1}{2}$

だから

$\alpha=\frac{2\pi}{3}$

また、

0≦θ≦2πより $\frac{2\pi}{3}$ ≦θ $+\frac{2\pi}{3}$ ≦ $\frac{8}{3}\pi$ の範囲をとります。

$2sin(\theta+\frac{2\pi}{3})=0$

$\theta+\frac{2\pi}{3}=\pi,2\pi$

$\theta=\frac{\pi}{3},\frac{4}{3}\pi$ になります。

②最小値、最大値を求める場合

三角関数の問題で、最大値、最小値を見たら、合成を疑いましょう。

今回はオーソドックスな問題と少し応用した問題を出題します。

Y=cosθ+sinθ

三角関数の合成を使って・・

= $\sqrt 2 sin(\theta+\frac{\pi}{4})$

0≦θ≦πより

$\frac{\pi}{4}$ ≦θ+ $\frac{\pi}{4}$ ≦ $\frac{5\pi}{4}$

最大値・・ $\theta+\frac{\pi}{4}=\frac{\pi}{2}$
⇒θ= $\frac{\pi}{4}$ の時

答え： $\sqrt 2$

最小値・・ $\theta+\frac{\pi}{4}=\frac{5\pi}{4}$
⇒θ=πの時

答え：-1

今回は、分かりやすい形で三角関数の合成を使う事が出来ましたが、加法定理や和積・積和の公式、三角関数の性質などを使って、最終的にAsinθ+Bcosθに持ち込む場合が多いです。

【応用】早稲田国際教養（類題）

4cos^２θ+2sin^２θ+2 $\sqrt 3$ sinθcosθ

の最大値、最小値を求める際三角関数の合成に持ち込めるか持ち込めないかが、勝負の分かれ目になります。

２倍角の公式の変形①： $cos^2 \theta=\frac{1+cos 2\theta}{2}$

２倍角の公式の変形②： $sin^2 \theta=\frac{1-cos 2\theta}{2}$

２倍角の公式の変形③： $2sin \theta cos \theta=sin2 \theta$

sin^２θやcos^２θを一乗にもっていく典型的な方法なので頭の中に入れといてください。

上記式を２倍角の公式を代入して、整理すると・・

$\sqrt 3 cos2\theta +sin2\theta +3$

になるので、後は、三角関数の合成を使うだけです。

応用問題のように、少し複雑になる場合もありますが、最終的にAsinθ+Bcosθに持っていかなくては合成は使えません。そのために、２倍角の公式がよく使われるので、こちらも頭の中に入れておいてください。

忘れている方はこちらをご覧ください。
『三角関数の基礎3　積和の公式&和積の公式』

アンケートにご協力ください！【利用状況に関するアンケート】

※アンケート実施期間：2023年4月5日～

受験のミカタでは、読者の皆様により有益な情報を届けるため、受験のミカタの利用状況についてのアンケート調査を行っています。今回はアンケートに答えてくれた方から10名様に500円分の図書カードをプレゼントいたします。

受験生の勉強に役立つLINEスタンプ発売中！

最新情報を受け取ろう！

プッシュ通知を許可する

受験のミカタから最新の受験情報を配信中！

この記事の執筆者

ニックネーム：受験のミカタ編集部

「受験のミカタ」は、難関大学在学中の大学生ライターが中心となり運営している「受験応援メディア」です。

三角関数の記事まとめストーリーで見る

人気記事ランキング合格サポート編ストーリーで見る

利用状況アンケート

受験のミカタ公式LINEを友だち追加する

プッシュ通知を許可する

人気のある記事

「数学」について