三角関数の加法定理とは？公式の覚え方と使い方・証明方法を解説！

数Ⅱ

数学 2024.6.24

「加法定理の公式は覚えたけど問題でどのように使うの？」「加法定理を使って三角関数の値の求め方を知りたい」とのように、三角関数の加法定理の公式は知っていても、実際の問題で正しい使い方が分からない方もいるでしょう。

加法定理は、高校数学Ⅱで学習する三角関数の重要単元です。国公立大学や私立理系大学の入試問題にも頻繁に出題されます。

加法定理の活用をマスターすることで、基本的な三角関数の問題から応用問題まで幅広く解くことができます。この記事を読んで加法定理を理解しましょう。

この記事で分かること
・加法定理の公式・証明方法
・加法定理を使った基本問題の解き方
・加法定理を使った応用問題の解き方

【PR】勉強を効率的に継続して、志望校に合格したい方必見！

↓無料ダウンロードはこちら↓

【目次】
1.三角関数の加法定理とは？
2.加法定理の公式と覚え方
　2-1.正弦（sin）の加法定理の公式
　2-2.余弦（cos）の加法定理の公式
　2-3.正接（tan）の加法定理の公式
　2-4.【発展】二倍角・半角・三倍角の公式
3.加法定理の証明方法
4.加法定理の問題の解き方・計算手順
5.加法定理の練習問題にチャレンジ！
　5-1.基本問題
　5-2.【発展】二倍角・半角を使う問題
　5-3.【発展】三倍角を使う問題
6.まとめ

三角関数の加法定理とは？

三角関数における加法定理は、2角の三角関数の値を用いて、2角の和/差から生まれる角の三角関数の値を求める公式のことです。

例えば、sin30°=1/2やsin45°=√2/2　といった三角関数の値はなじみあるものだと思います。一方、30°と45°を足し合わせたsin75°の値を覚えている人は少ないのではないでしょうか。

そんな時、加法定理を活用することによって、sin30°=1/2やsin45°=√2/2　といった既知の情報を用いながらsin75°の値を計算で導出することができます。

加法定理の公式と覚え方

加法定理は、正弦（sin）・余弦（cos）・正接（tan）のそれぞれに対して公式が存在します。まずは、３つの公式を確認してみましょう。

これらの定理を使うことで、数学Ⅰで学習した三角比30°・45°・60°の和と差で表せる角度の三角比の値を求めることができます。

しかし、加法定理の問題を解くためには加法定理の公式を覚える必要があります。sin、cos、tanそれぞれの公式を詳しく解説します。

正弦（sin）の加法定理の公式

正弦（sin）の加法定理の公式は左辺と右辺の符号の変化はなく、α+βを足した（引いた）ときの正弦（sin）は、sinαcosβとcosαsinβを足した（引いた）値となります。

正弦（sin）の加法定理の公式を用いてsin⁡θを求める問題がよく出題されます。公式の覚え方の一つに語呂合わせがあります。

という語呂合わせで覚えましょう。

余弦（cos）の加法定理の公式

余弦（cos）の加法定理の公式は、左辺と右辺で符号が逆になるため注意です。

余弦（cos）の加法定理の公式を用いて、cos⁡θを求める問題がよく出題されます。

公式の語呂合わせは

で覚えましょう。

正接（tan）の加法定理の公式

正接（tan）の加法定理の公式を用いて、tan⁡θを求める問題がよく出題されます。

正接の加法定理の語呂合わせは
tan⁡(α+β)の場合、分母、分子の順に「1枚（－）タンタン、タンプラタン」
と覚えます。

正接の加法定理は、正弦・余弦とともにかならず覚えてほしい公式ですが、特に複雑で使用する頻度も少なく、忘れてしまう場合が多いです。

そこで、公式を忘れても対処できるよう、正弦の加法定理と余弦の加法定理を使って正接の加法定理を導出する方法を知っておきましょう。手順は以下の通りです。

【発展】二倍角・半角・三倍角の公式

加法定理を使用すると、二倍角、半角、三倍角の公式が得られます。30°・45°・60°の定数倍の角度の三角比の値を簡単に求めることができます。

例えば、sin⁡120° の値を求めたいとき120°は、60°の二倍角なので、二倍角の公式にα=60°を代入して計算します。

したがってsin⁡120°=√3/2と求めることができます。

加法定理の証明方法

ここまで加法定理の公式を確認してきました。

この章では加法定理が成り立つ経緯を説明するために、加法定理の証明を行っていきます。東京大学の入試で出るくらい重要な証明なので、ぜひ証明方法をここで確認し、理解を深めておきましょう。

証明にあたってグラフを使っていきます。

下図のように、半径が1の円周上に2点P, Qをとります。

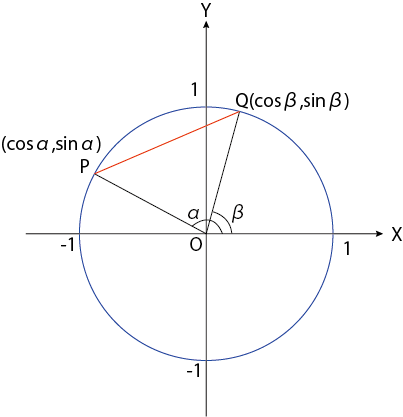
この時、PQの長さは２通りの方法で表現することができます。

1つ目は距離の公式です。

PQ²=(cos⁡α-cos⁡β)²+(sin⁡α-sin⁡β)²

右辺を展開して整理すると、

PQ²=(cos⁡α-cos⁡β)²+(sin⁡α-sin⁡β)²=2-2(cos⁡αcos⁡β+sin⁡αsin⁡β)・・・③

2つ目は三角形POQに注目した余弦定理の式です。（忘れた方は「▶５分でわかる！余弦定理の公式と証明、使い方を簡単に理解しよう！」をご覧ください。）

PQ²=OP²+OQ²-2OP・OQ・cos⁡∠POQ
=1²+1²-2×1×1×cos⁡(α-β)
=2-2cos⁡(α-β)・・・④

③と④を連立させると、

2-(2cos⁡αcos⁡β+sin⁡αsin⁡β)=2-2cos⁡(α-β)
cos⁡(α-β)=cos⁡αcos⁡β+sin⁡αsinβ・・・⑤

⑤の左辺をsin(α+β)に変換します。そのために三角関数の性質を使います。

$cos(\theta+\frac{\pi}{2})=-sin\theta$

・・・⑥
$cos(\theta-\frac{\pi}{2})=sin\theta$

・・・⑦
$sin(\theta+\frac{\pi}{2})=cos\theta$

・・・⑧

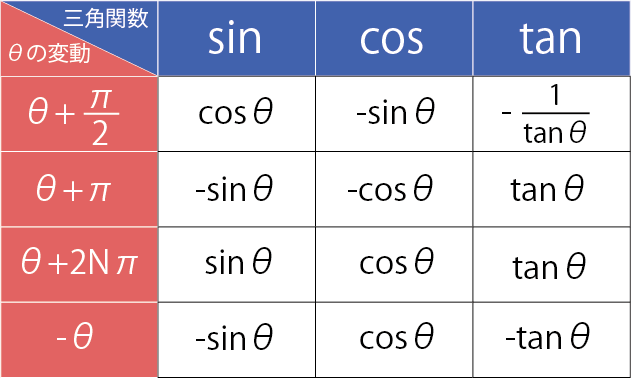
の性質を使って、cos⁡(α-β)=cos⁡αcos⁡β+sin⁡αsinβのβをβ+ $\frac{\pi}{2}$ に置き換えます。

$cos[\alpha-(\beta+\frac{\pi}{2})]=cos\alpha cos(\beta+\frac{\pi}{2})+sin\alpha sin(\beta+\frac{\pi}{2})$

上記の⑥～⑧で変換すると、

sin(α-β)=sinαcosβ-cosαsinβ

になります。

あとはβ=-βに置き換えて

sin(α+β)=sinαcosβ+cosαsinβ

が証明出来ます。

加法定理の問題の解き方・計算手順

ここからは、実際に加法定理の問題を解くための手順を紹介していきます。一つ一つ手順を確認しながら、一緒にsin⁡75°の値を求めていきましょう。

まず、いきなりsin⁡75°の値を求めることはできません。そこで、正弦の加法定理を思い出しながら、α+β=75またはα-β=75　となるα、βの値がないかを考えます。
この時、α、βの値を30や45°、60°や90°など定番の角度に設定することがポイントです。

今回の場合、α=30°、β=45°とおいてあげると加法定理が使えそうですね。sin30° =1/2、 cos45°=√2/2、cos30°=√3/2、 sin45°=√2/2であることから、加法定理を用いて、

となります。

加法定理の練習問題にチャレンジ！

では実際に加法定理の練習問題を解いてみましょう。基礎問題から発展問題まで、自分の今の理解度にあわせて解き進めてみてください。

基本問題

【問題1】
cos⁡105° の値を求めなさい。

【解答解説】
105°=45°+60°であるから、余弦（cos）の加法定理の公式を使います。

cos(α+β)=cos⁡αcos⁡β-sin⁡asin⁡β

α=45° 、β=60°とおいて代入。

cos(45+60°)=cos45°⁡cos60°⁡sin⁡45°sin⁡60°

つまり、

と求まります。

【問題2】
tan15° の値を求めなさい。

【解答解説】
15°=45°-30°であるから、正接（tan）の加法定理の公式を使います。

tan(α-β)=(tanα-tanβ)/(1+tanαtanβ)

α=45° 、β=30°とおいて代入することで、求めることができます。

cos15°
＝cos(45°－30°)
＝cos45° cos30° + sin45° sin30°

＝
= …（答）

【発展】二倍角・半角を使う問題

【問題3】
π/2<θ<π、sinθ=3/5 のとき、cos2θの値とsin2θの値を求めなさい。

【解答解説】
余弦（cos）の二倍角の公式「cos2θ＝1－2sin²θ」を使いましょう。

この式にsinθ=3/5 を代入し、

cos2θ
＝1－2sin²θ
＝1－2・(3/5)²＝１－(18/25)
＝7/25…（答）

また、π/2<θ<πであるから、

cosθ
＝－

=－

=－4/5 …①

ゆえに、

sin2θ
= 2sinθcosθ
＝ 2・3/5・(－4/5)
＝－24/25 …（答）

【発展】三倍角を使う問題

【問題4】
sin3θ=3sinθ－4sin³θとなることを証明せよ

【解答解説】
sin3θをsin(2θ+θ)と考えましょう。

sin3θ
= sin(2θ+θ)
= sin2θcosθ + cos2θsinθ（加法定理）
= 2sinθcosθ・cosθ + (1－2sin²θ)・sinθ
= 2sinθ(1－sin²θ) + sinθ－2sin³θ
= 3sinθ－4sin³θ

まとめ

最後までご覧いただきありがとうございました。この記事では、加法定理の公式や練習問題について、基礎知識と考え方を確認しながら解説しました。

加法定理を攻略するコツは、頭の中に単位円のイメージを持っておくことです。
加法定理の公式は複雑なため目の前の式や数字に意識が向いてしまいますが、あくまで「単位円にある点の座標を考える」という図形問題であることを意識しておくと、頭の中が整理されますよ。

そして加法定理を使いこなすためにはまず、三角比や三角関数の問題になれることが重要です。
受験のミカタでは三角比や三角関数に関する記事を多数公開しているので、適宜参照して得意分野にしてください。

アンケートにご協力ください！【利用状況に関するアンケート】

※アンケート実施期間：2023年4月5日～

受験のミカタでは、読者の皆様により有益な情報を届けるため、受験のミカタの利用状況についてのアンケート調査を行っています。今回はアンケートに答えてくれた方から10名様に500円分の図書カードをプレゼントいたします。

受験生の勉強に役立つLINEスタンプ発売中！

ニックネーム：受験のミカタ編集部

「受験のミカタ」は、難関大学在学中の大学生ライターが中心となり運営している「受験応援メディア」です。

三角関数の加法定理とは？