加法定理問題　二倍角・半角・三倍角の解き方がすぐわかる！

今回は加法定理の問題を扱います。

sin(α+β)の基本形から、二倍角・半角、三倍角まで網羅してあります！

それでは、さっそくチャレンジ！

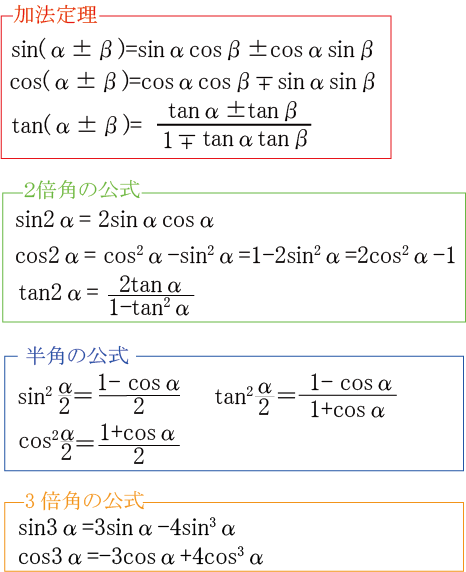
※公式一覧

加法定理 証明・簡単な覚え方・語呂合わせより

 

 

 

１．加法定理問題＆解説【基本】

【問題】

cos15°の値を求めよ。

 

【解答＆解説】

cos15°

＝cos(45°－30°)

＝cos45° cos30° + sin45° sin30°

＝

=  …（答）

 

２．加法定理問題＆解説【二倍角・半角】

【問題(1)】

cos2θの値を求めよ。

また、sin2θの値も求めよ。

 

【解答＆解説】

cos2θ

＝1－2sin²θ

＝1－2・(3/5)²

＝１－(18/25)

＝7/25…（答）

また、

π/2 < θ < π であるから、

cosθ

＝－

=－

=－4/5 …①

ゆえに、

sin2θ

= 2sinθcosθ

＝ 2・3/5・(－4/5)

＝－24/25 …（答）

 

【問題(2)】

 

 

【解答＆解説】

π/2 < θ < πより、

π/4 < θ/2 < π/2 であるから、

tanθ/2 > 0 である。

よって、

tanθ/2

=   (①よりcosθ=－4/5)

= 3 …（答）

 

３．加法定理問題＆解説【三倍角】

【問題】

sin3θ=3sinθ－4sin³θ

となることを証明せよ。

 

【解答＆解説】

sin3θをsin(2θ+θ)と考えましょう。

sin3θ

= sin(2θ+θ)

= sin2θcosθ + cos2θsinθ（加法定理）

= 2sinθcosθ・cosθ + (1－2sin²θ)・sinθ

= 2sinθ(1－sin²θ) + sinθ－2sin³θ

= 3sinθ－4sin³θ

 

いかがでしたか？？

加法定理の公式の証明方法や、簡単な覚え方や語呂合わせを知りたい人はこちらをご覧ください

⇒ 加法定理 証明・簡単な覚え方・語呂合わせ

 

この記事の執筆者

ニックネーム：やっすん

早稲田大学商学部4年
得意科目：数学