ヘロンの公式とは？使い方・証明方法を解説！練習問題付き

1ヘロンの公式は、三角形の３辺の長さが全てわかっているときに、三角形の面積を直接計算できる便利な公式です。

使い方がわかるととても便利なヘロンの公式ですが、
「ヘロンの公式ってどんな時に使うの？」といった高校生の戸惑いの声はよく耳にします。

ヘロンの公式はあくまでも「発展編」扱いで、授業でも軽く触れる程度というケースもあるでしょう。
そのため、ヘロンの公式はいまいち浸透していないのかもしれません。

この記事では、ヘロンの公式の使い方と練習問題を用意しているので、数学が苦手な人でも記事を通して理解が進むはずです！

三角関数の公式の理解に役立つ記事のまとめもぜひ参考にしてみてください！

ヘロンの公式とは？

ヘロンの公式は、三角形の面積を求める際に利用できる公式です。証明がやや複雑なため、その場で導出するよりは、公式を暗記しておくのがおすすめです。

まずは、公式を使う場面や式の意味を解説していきます。

三角形の3辺の長さから面積を求める公式

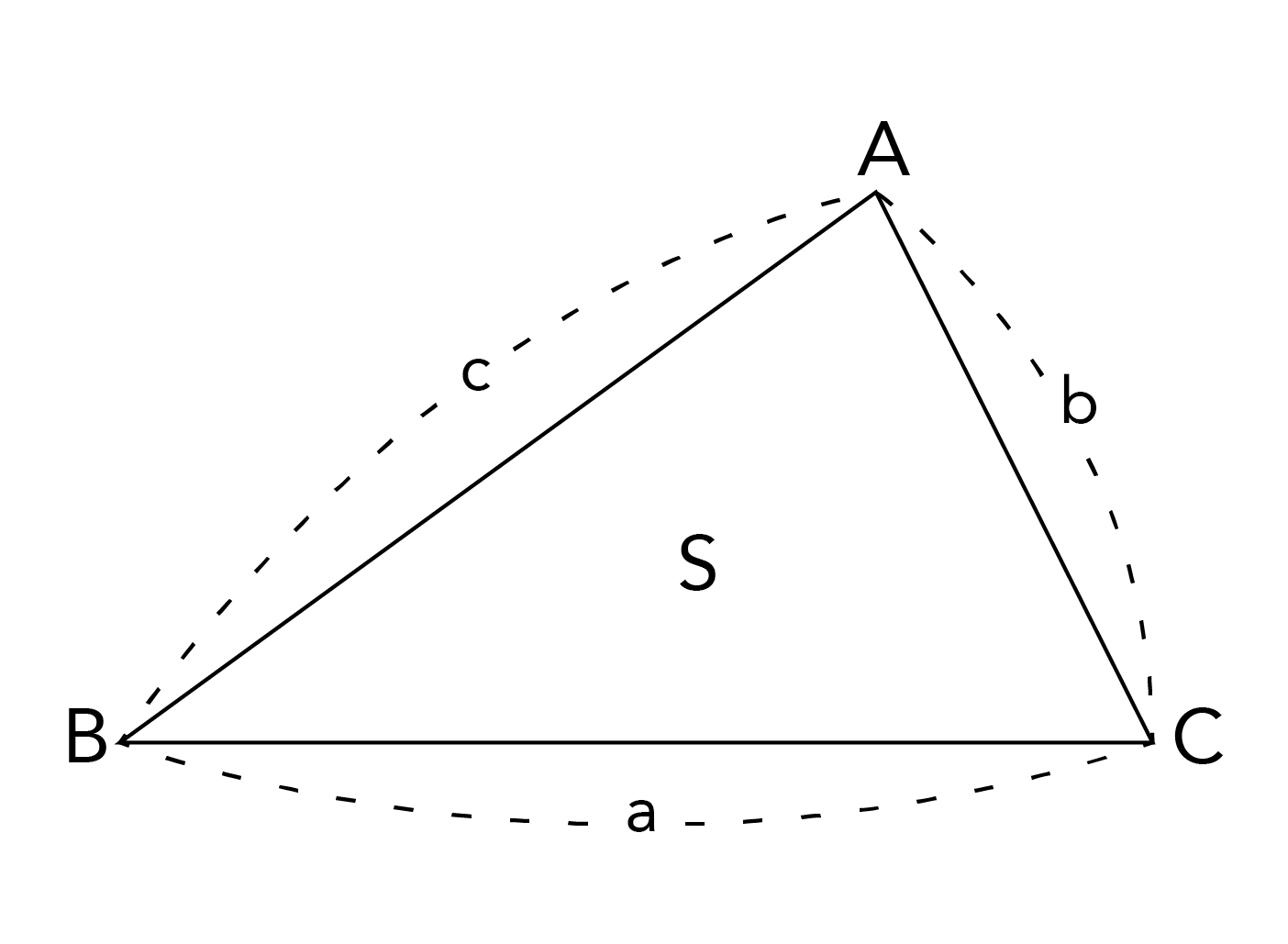
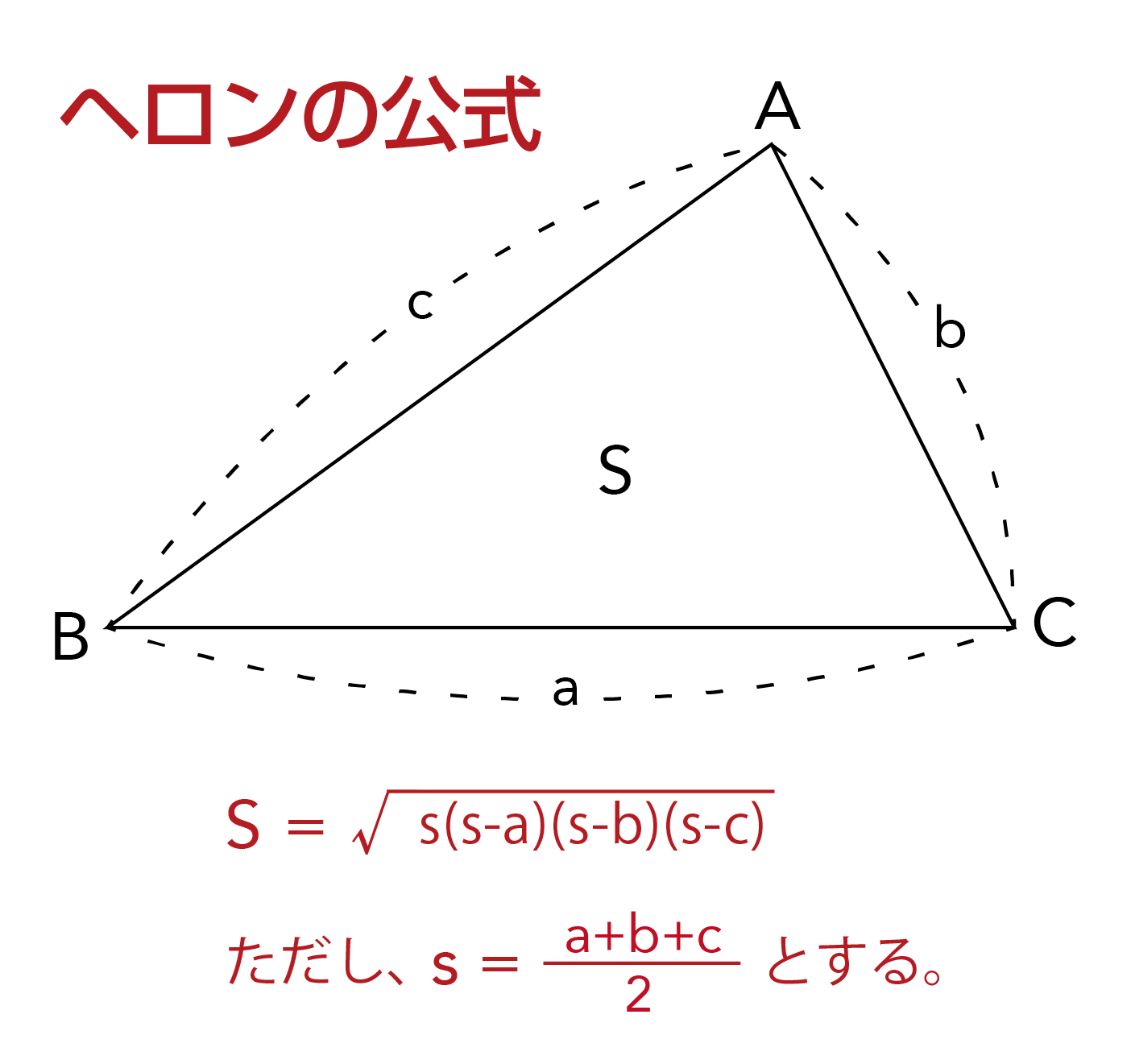
下の図のように、３辺の長さがa,b,cの三角形ABCの面積Sを考えます。

ヘロンの公式を用いると、以下のように三角形の面積を求めることができます。

ヘロンの公式は以下のように2段階に分けることができます。

このように、三角形の3辺の長さが分かっていれば、ヘロンの公式を使って三角形の面積を計算できるのです。

ヘロンの公式はとても便利なので、必ず覚えておきましょう。

ヘロンの公式の使い方

それでは具体的な例を用いて、ヘロンの公式を使って見ましょう。
たとえば、a=5, b=6, c=7である△ABCの面積Sを求めます。

「s=(a+b+c)/2」のsを求める

まずは、3辺の長さを用いて、ｓ=(a+b+c)/2の値を求めます。

※ここでsは、△ABCの周の長さの半分を表しています。

sを公式に代入して面積を求める

sの値が求まったら、ヘロンの公式にｓの値を代入すると、面積Sが計算できます。

 

これで、△ABCの面積が求められました。

ヘロンの公式の証明

では、先ほど紹介したヘロンの公式を証明していきます。

ヘロンの公式の証明は、必ずしも覚える必要はありません。しかし、三角関数の基礎や余弦定理について復習できる良い機会です。

以下の図のように、三角形ABCの面積Sを考えていきましょう。

まず、三角形ABCの面積Sは、2辺とその間の角を使って、

と表すことができますね。

ここでsin²θ= 1 – cos²θを利用して、

（詳しくは、三角関数の基礎について解説した記事をご覧ください。）

 

となります。

ここで、

が成り立つので、

（余弦定理があまり理解できていない人は、余弦定理について解説した記事をご覧ください。）

ここからは、√の中をきれいにまとめていくのですが、ここで因数分解の公式

を多用していきます。

√の中は４つの因数の積の形になりました。これらは全てa, b, cを含む式となっているので、これをもう少しまとめてみます。ここで、

とおきます。これはつまり、

と表すこともできます。
そこで、先ほどの式に対してsを用いて次のように変形をします。

式が何となくまとまってきた感じがしますね。さらに次のようになります。

これでヘロンの公式が証明されました。

少し複雑でしたが、ヘロンの公式の証明は必ずしも覚える必要はありませんので安心してください。

ヘロンの公式の証明は以上になります。

【発展】ベクトルを用いた証明

すでにベクトルを学習している方は、ヘロンの公式の証明として、ベクトルを用いてアプローチすることも可能です。

ベクトルは「向きと大きさをもつ量」であり、数学Bで習う単元です。

ベクトルを既に習ったけれど忘れてしまったという方は、「ベクトル記事まとめ」をご活用ください。

証明は次のとおりです。

これは先ほどの証明でも出てきた式です。
ここから、先ほどと同様に√の中をsを用いてまとめていきます。

練習問題：三角形の面積を求める

それでは、具体的な問題を解いてみましょう。

問題

a=7、b=4、c=5の三角形ABCの面積Sを求めよ。

ヘロンの公式を用いた解き方

まずは、これまで学んできたヘロンの公式を使って面積を求めてみましょう。

解答&解説

ヘロンの公式を利用しましょう。

まず、sの値を求めます。

よって、求める三角形の面積Sは、

ヘロンの公式を知っていれば、3辺の長さがわかっている三角形の面積を求めることは比較的簡単です。公式をしっかりと覚えておきましょう。

余弦定理を用いた解き方

もしヘロンの公式を忘れてしまった場合は、余弦定理を用いることでも面積の計算をすることができます。
同じ問題で、解き方を紹介しましょう。

三角形の情報としては3辺の長さのみですから、正弦定理を利用できません。

そこで、余弦定理が使えるか考えてみましょう。

余弦定理には上記3種類の公式があります。いったいどれを使うと賢いでしょうか？
この判断のポイントは、公式の分母の部分です。いずれも2辺の長さの積が含まれています。

分数計算は約分できれば計算が楽になるため、分母には約分しやすい数が来た方がいいですよね。

今回の場合は、４や５が分母に来た方が良いと判断する人が多いでしょう。ですから、cosA＝～の公式を使ってみましょう。

三角形の面積計算ではsinの値が必要です。相互関係の公式を利用して、cosの値を変換します。

最後に三角形の面積の公式に当てはめます。

ヘロンの公式で計算した面積と一致しました（当然ですが）。
こちらはヘロンの公式による解法と比べ、使用する公式や計算量が多い印象があるでしょう。

ヘロンの公式の便利さがお分りいただけましたか？ヘロンの公式を使えば、解答の時間の短縮にもなります。

ぜひこの記事で、ヘロンの公式をマスターしておきましょう！

3辺の長さが分からない場合は他の公式を使う

高校数学では、問題に応じて様々な三角形の求積公式を使い分ける必要があります。

ここでは、高校までに学ぶ三角形の面積の計算公式をまとめてみました。知らなかった公式があれば、ぜひ覚えて使えるようになってください！

基本公式

三角形の面積を求める方法として、最初に学ぶのがこの基本公式です。小学校で学びますね。底辺と高さの2つの要素から求められます。

三角比の面積公式

次に、三角比を利用して、三角形の面積を求める方法です。2辺とその間の角の情報を利用します。

内接円の半径

三角形ABCの内接円の半径と、3辺の長さから求めることができます。

証明は以下のとおりです。

外接円の半径

高校数学ではどちらかといえば内接円の半径を用いた面積計算はよく取り上げられる一方、外接円の半径を用いた次の公式は暗記事項には含まれておらず、知らない高校生も多いでしょう。

証明は以下のとおりです。

この公式は、三角形の3辺の長さおよび外接円の半径がわかっていなければ求めることができません。3辺の長さがわかっているなら、ヘロンの公式でも計算できるとお気づきの方も多いでしょう。

したがってこの公式は、三角形の面積を計算するためよりも、先に三角形の面積を求めてから、外接円の半径を求めるために利用することが多いです。

ベクトルを用いる

前述した「ヘロンの公式の証明」の中の「ベクトルを用いた証明」で、次の式を書きました。

これはさらに内積の定義式により、

と表すことができます。

ベクトルの成分表示

上記のベクトルにおいて、成分表示されている場合は次の公式を使用できます。

証明は以下のとおりです。

この公式は、ベクトルが成分表示できる場合や、平面座標で頂点の座標が表される場合に有効です。なお平面座標の場合、どれか一つの頂点が原点であるか、原点になるよう平行移動する必要があります。

まとめ

三角形の面積を求める計算は、高校数学の様々な場面で求められます。公式を場面に応じて適切に使い分けられれば、効率よく問題を解くことができるでしょう。

今回はやや応用的な公式である、ヘロンの公式を解説しました。
ヘロンの公式、三角形の面積を求める公式の使い分けがマスターできるよう、繰り返し復習しましょう！