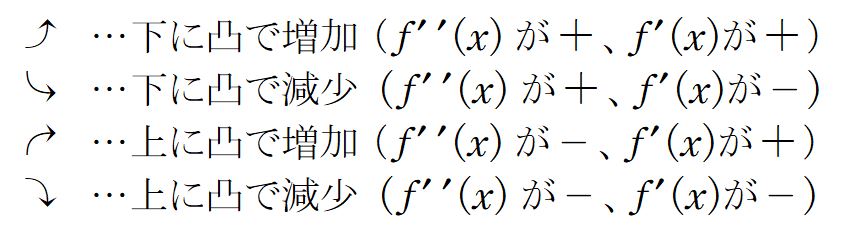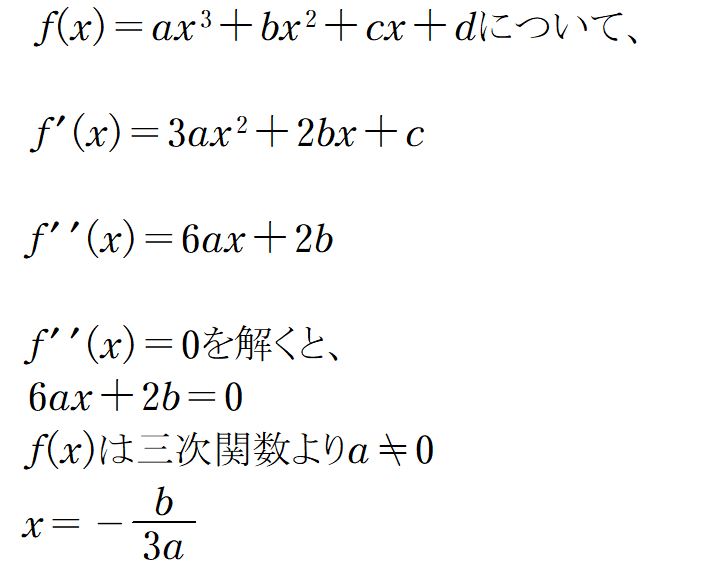変曲点とは？変曲点の定義や求め方を分かりやすく解説！

変曲点を求める方法は知っていても、「そもそも変曲点とは何か」という疑問や「変曲点そのものを求める方法を忘れてしまった」というケースがあるでしょう。

変曲点は関数のグラフの曲がり方が変わる点のことです。増減表を書き、グラフを描くことで変曲点が分かります。

様々な関数について、変曲点の求め方を例題をもとに解説します。変曲点を理解すれば関数の値の変化が分かり、微分の問題が解けるようになります。

高校数学の微分の基本ともいえる変曲点の定義・求め方をマスターし、様々な微分の問題を解けるようにしていきましょう。

【PR】勉強を効率的に継続して、志望校に合格したい方必見！

↓無料ダウンロードはこちら↓

変曲点の基本的な定義・意味

さまざまな関数のグラフを考えるときに、その変化を把握するためには、「上に凸」や「下に凸」などの「グラフの曲がり方」を正確にとらえる必要があります。

そこで、「変曲点」という概念を知っておくと便利です。変曲点とはどのような点のことをいうのでしょうか。その定義やグラフ上の意味について解説します。

変曲点とは「グラフの曲がり方が変わる点」のこと

変曲点は、読んで字のごとく、y＝f(x)のグラフの曲がり方が変化を起こす点のことを指します。

関数f(x)があり、それは二階微分可能（導関数f’(x)の導関数f’’(x)が求められる）で、かつそれが連続である（値が途切れない）であるとします。

そのとき二階微分f’’(x)はxについての関数となるので、xの値の変化にしたがってf’’(x)の値は変化します。その中で、f’’(x)の符号が変化する点のことを「変曲点」とよびます。詳細を次に説明しましょう。

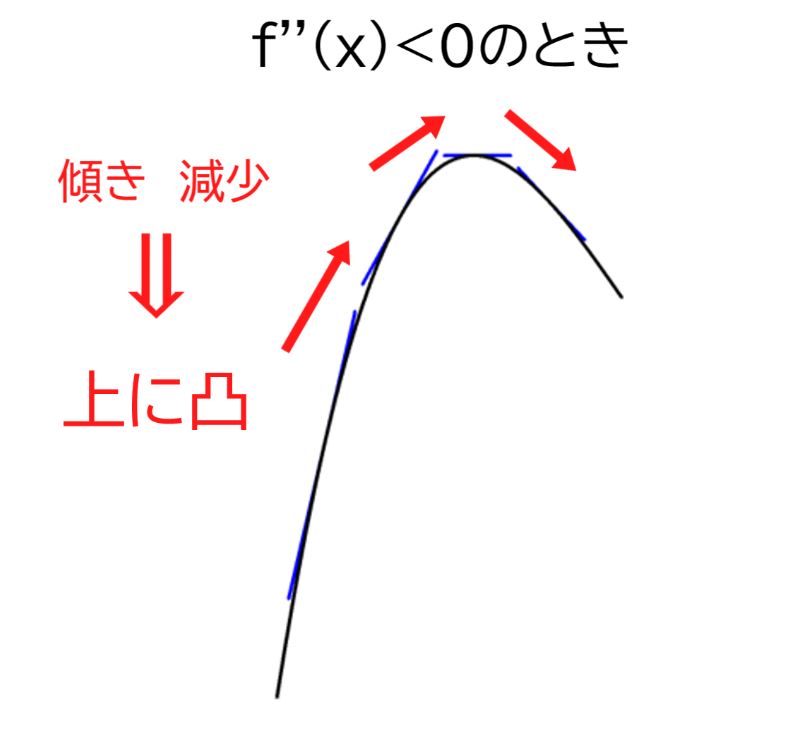
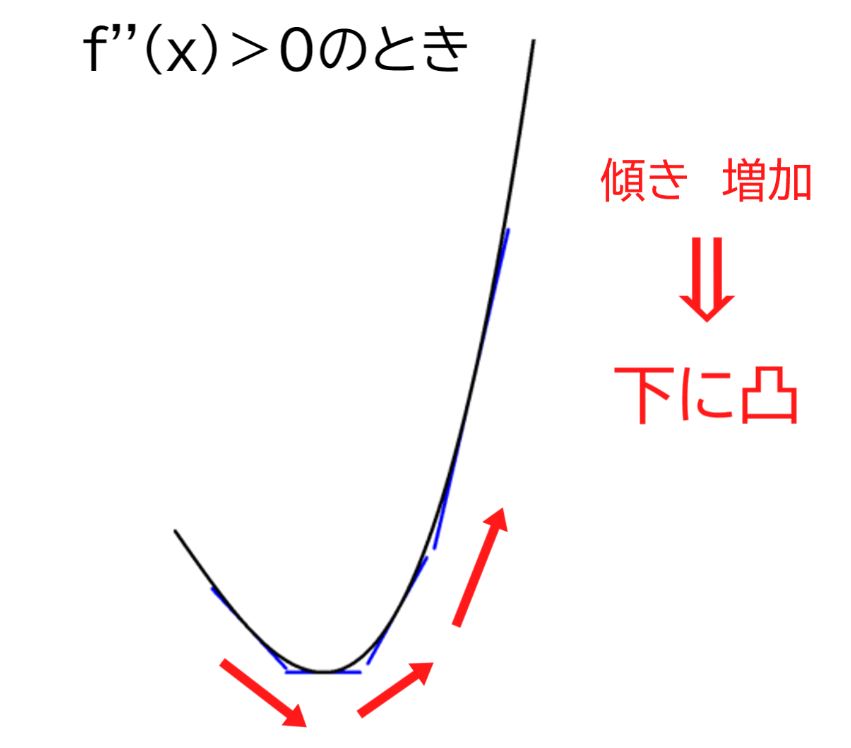
f”(x)＜０ならグラフは上に凸、f”(x)＞０なら下に凸

そもそもf’’(x)は何を意味するのでしょうか。

f’’(x)は、f’(x)の導関数であることから、f’(x)の増加や減少を表します。

これは、f(x)の増加・減少が、その導関数ｆ‘（ｘ）の符号によって決まることと同じです。

つまり変曲点というのは、f’’(x)の符号が切り替わるf’’(x)＝0となるとき、y＝f(x)のグラフで「上に凸」と「下に凸」が切り替わる地点であることを意味します。

また、接線の傾きで「増加」と「減少」が切り替わる地点であるということでもあります。

変曲点の求め方

変曲点のグラフでの特徴は今説明した通りです。関数y＝f(x)が与えられたときに変曲点を求めるまでの手順はどのようになるのかについて知る必要があります。次にその求め方について解説します。

f”(x)=0をxについて解く

変曲点は関数f(x)の二階微分f’’(x)の符号が切り替わるときの場合がわかればよいのです。すなわちまずはf’’(x)＝0となる場合を求めてみることから始めます。

関数f(x)を微分してf’(x)を、そしてそれをさらに微分してf’’(x)を求めます。

xについての方程式f’’(x)＝0を解きます。

ただし、ここで気をつけなければならないことは、f’’(x)＝0のとき、必ずしもその前後でf’’(x)の符号が切り替わるとは限らないということです。

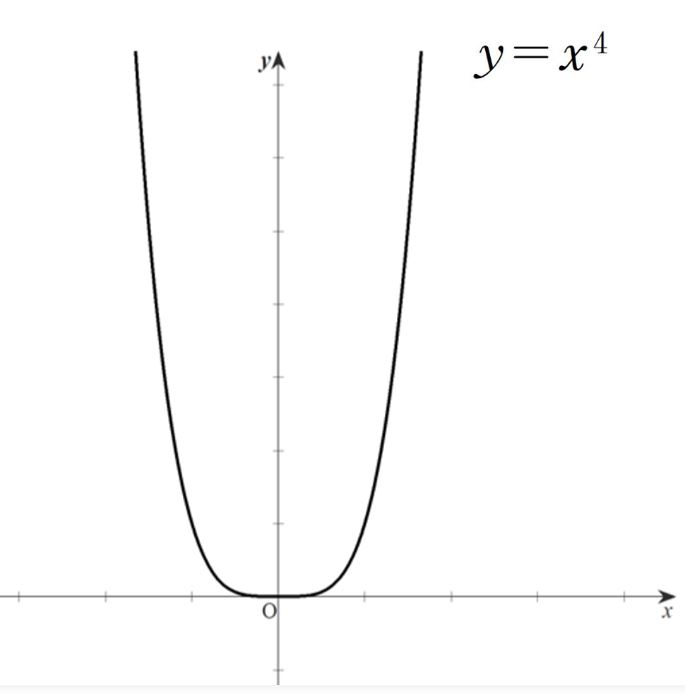
たとえばf(x)＝x⁴の場合、

となり、f’’(x)＝0となるのはx＝0のときであるとわかりますが、ｘが負のときも正のときもf’’(x)＞0となり、f’’(x)＜0である場合が存在しません。

つまりf’’(x)の符号が切り替わらないので、ｙ＝f(x)のグラフには変曲点はないといえます。


【上図】y＝x⁴のグラフ。終始「下に凸」の形をしており、変曲点は存在しない

ですから、f’’(x)＝0を解いて、それをみたすxが見つかっても、その前後のf’’(x)の符号を調べる必要があります。

その方法が、「増減表を書く」ということです。

増減表を書く

変曲点があるかどうかを見極め、関数の値の変化をきちんと押さえきれなければ、正しいグラフを描くことはできないでしょう。それを実現するには増減表を書くことです。

数学Ⅱの「微分法」の際には、増減表は上から「xの値」「f’(x)の符号」「f(x)の値および増加・減少」を書きました。それと同じように、増減表を作っていくわけです。

今回はf’’(x)の欄を新たに設けるため、上から「xの値」「f’’(x)の符号」「f’(x)の符号」「f(x)の値およびグラフの凹凸と増加・減少」と、4段からなる表を書くことになります。

たとえば、3次関数y＝x³＋3x²-9xの場合は次のようになります。

※増減表のf(x)の欄の矢印は次のように使用します。


y＝f(x)のグラフは次のようになります。

変曲点の性質

関数によって変曲点のもち方はそれぞれに決まります。次に変曲点の性質について紹介をします。

三次関数の変曲点は、1個しか存在しない

次の三次関数f(x)について考えてみましょう。


f(x)は一次関数なので、この値を境に前後で符号が入れ替わる。

したがってｆ（ｘ）の変曲点は存在し、その個数は1個だけである。

【例題１】

四次関数の変曲点は、0個か2個存在する

次に、四次関数の場合は、変曲点は何個存在するのかを考えてみましょう。

f(x)が四次関数であるとき、f’’(x)の次数は2下がるので二次関数となります。

「二次方程式」で学びましたが、f’’(x)=0を満たす実数は、「異なる2個」「1個（重解）」「実数はない」の3通りが考えられます。そのそれぞれにおける変曲点のもち方は次のとおりです。

したがって、四次関数の変曲点の個数は0個か2個であることがわかります。

また、四次関数が変曲点を2個もつための条件は

【例題２】

【例題３】

《註》
※③の部分の、変曲点の個数を判断する部分は、②からf’’(x)=0が異なる2個の実数解をもつことが明白なので、それを示した上で変曲点を2個もつことをいってもよいです。

※実際のy=f(x)のグラフは、①でf’(x)=0を解く際に、次のようになります。

2つの実数解が無理数の複雑な値をとるため、増減表からグラフを描くという作業が面倒なケースとなります（特にf(x)の値）。

様々な関数の変曲点を求めてみよう

三次関数や四次関数を例に紹介してきましたが、次にさまざまな関数を通して変曲点を考えてみましょう。

三角関数

【例題４】

その他の関数

次にlogを用いた関数の変曲点について求めていきます。

【例題5】

まとめ

数学Ⅲの微分法において、さまざまな関数を使用するようになります。その際、値の変化あるいはグラフの形状を正確にとらえるためには、変曲点を知っておかなければなりません。

変曲点は、f’’(x)の符号（正と負）が切り替わるところであり、「上に凸」と「下に凸」が切り替わる点です。増減表を利用するなどして、f(x)の変化をつかめるよう練習をしていきましょう。