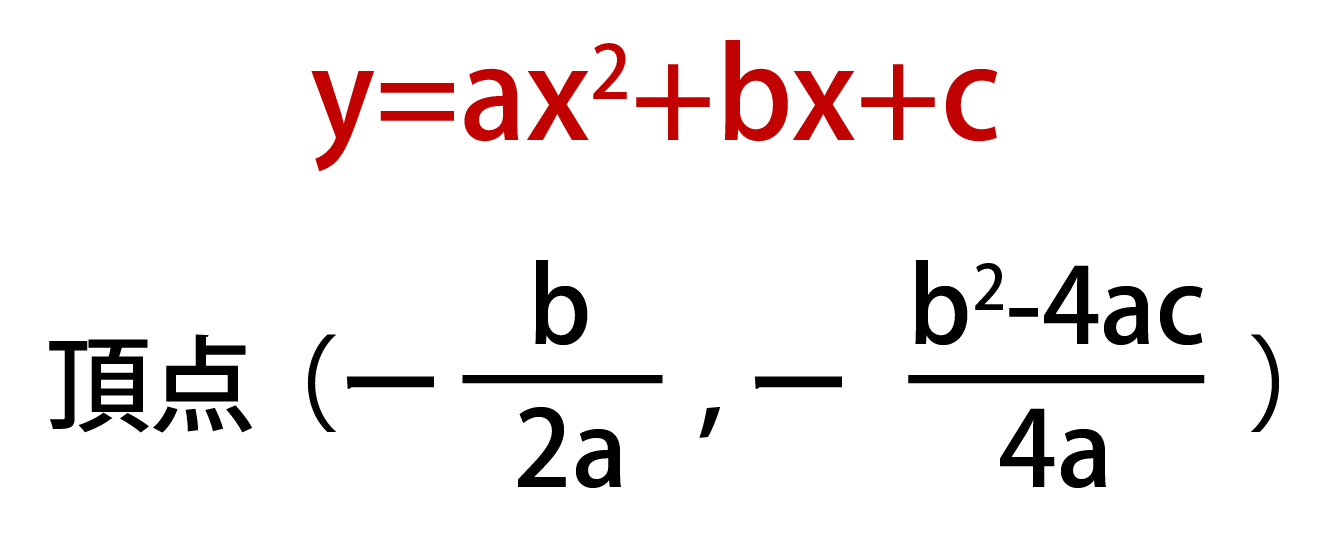二次関数グラフの書き方＆頂点を一発で求める方法とは？

二次関数のグラフの書き方・解き方（二次関数のグラフを平行移動させる方法）について、スマホでも見やすいイラストを使って現役の早稲田大生が解説します。

この記事を読めば、二次関数のグラフがスラスラ書けるようになっているでしょう。

また、二次関数のグラフの学習において、知っておくと便利な知識（二次関数のグラフで頂点を一発で求めるための公式）も紹介します。

ぜひ最後までご覧ください。

【PR】勉強を効率的に継続して、志望校に合格したい方必見！

↓無料ダウンロードはこちら↓

 

１：二次関数グラフの書き方

まずは二次関数のグラフの書き方を、スマホでも見やすいイラストを使いながら解説します。

二次関数(y=ax²+bx+c)には、下に凸なグラフ(a>0の場合)と、上に凸なグラフ(a<0の場合)の２つがあるので、順番に解説していきます。

 

下に凸な二次関数グラフの書き方

y=x²-4x-12という二次関数のグラフを例にとり、グラフを書く方法を解説します。二次関数のグラフの書き方は、主に４ステップです！

 

【手順１：平方完成をする】

まずは、グラフを書きたい二次関数を平方完成します。

※平方完成のやり方がわからない人は、平方完成のやり方について詳しく解説した記事をご覧ください。

y=x²-4x-12を平方完成すると、

y=(x-2)²-16となりますね。

 

【手順２：頂点を求める】

平方完成して、y=(x-p)²+qの形に変形できれば、頂点を求めましょう。

y=(x-p)²+qのグラフの頂点の座標は、(p,q)となります。

※二次関数の頂点について深く学習したい人は、二次関数の頂点について詳しく解説した記事をご覧ください。

したがって、先ほど平方完成した

y=(x-2)²-16というグラフの頂点の座標は(2,-16)となります。

【手順３：y=0の時のxの値を求める】

頂点の座標が求まったら、次は二次関数のyの値が0の時のxの値を求めます。

今回書きたい二次関数のグラフはy=x²-4x-12なので、

0=x²-4x-12という式を考えて、xの値を求めます。

右辺を因数分解しましょう。

※因数分解があまり理解できていない人は、因数分解のやり方について詳しく解説した記事をご覧ください。

（右辺）

= (x+2)(x-6)

なので、x=-2 , 6です。

よって、x軸上に(-2,0)と(6,0)を書きます。

 

【手順４：下に凸のなめらかな曲線を書く】

以上で3点が決まりました。最後は、この３点を通る下に凸なグラフをなめらかなに書きましょう。

これで二次関数のグラフが書けました。次は、上に凸な場合の二次関数のグラフの書き方を解説します。

 

上に凸な二次関数グラフの書き方

上に凸な二次関数のグラフの書き方も、先ほどの手順とほぼ同じです。

今回は、y=-x²+8x-15というグラフを例にとり解説します。

 

【手順１：平方完成をする】

まずは平方完成をします。

y=-x²+8x-15を平方完成すると、

y=-(x-4)²+1となりますね。

 

【手順２：頂点を求める】

y=-(x-4)²+1より、グラフの頂点の座標は(4,1)ですね。

※二次関数の頂点について深く学習したい人は、二次関数の頂点について詳しく解説した記事をご覧ください。

 

 

【手順３：y=0の時のxの値を求める】

y=0の時のxの値を求めましょう。

0=-x²+8x-15より、

（右辺）

=-(x-3)(x-5)なので、

x=3 , 5のときにy=0となります。

点(3,0)と(5,0)を座標上にとりましょう。

 

【手順４：上に凸のなめらかな曲線を書く】

以上で３点が決まったので、この３点を通る上に凸なグラフをなめらかに書きましょう！

これで上に凸なy=-x²+8x-15のグラフが書けました。

二次関数のグラフの書き方の解説はこれで終わりです。次の章では、二次関数のグラフの平行移動について解説します。

 

２：二次関数グラフの解き方（平行移動）

二次関数のグラフ学習では、グラフを平行移動させるという機会が多く登場します。

この章では、平行移動の解き方（２パターンあります）について解説します。

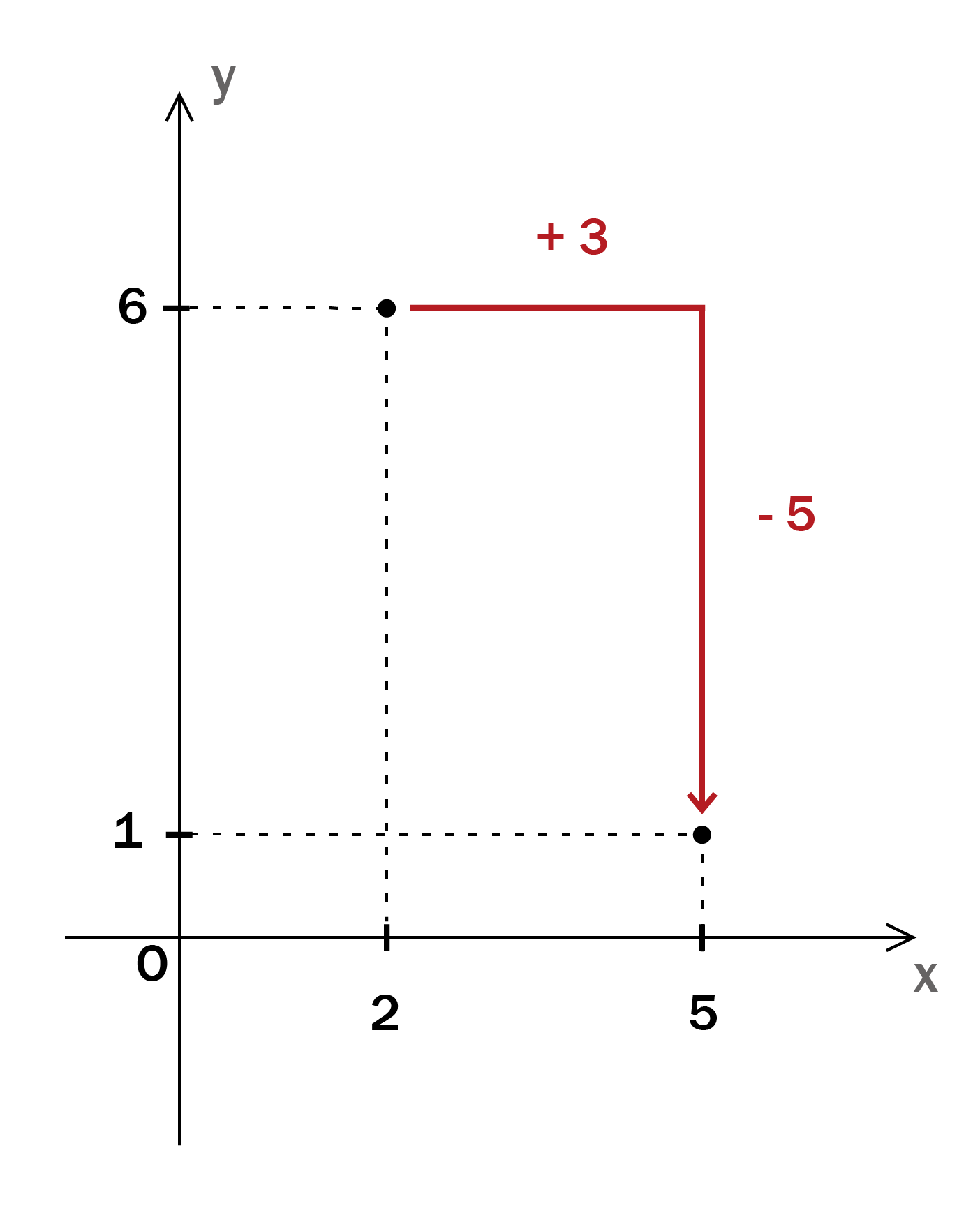
例えば、y=x²-4x+10という二次関数のグラフを、x軸方向に3、y軸方向に-5平行移動させる場合を考えてみます。

 

平行移動の解き方：その１

１つ目解き方は、平方完成を利用する方法です。

まずは平行移動させたい二次関数を平方完成します。

y=x²-4x+10を平方完成すると、

y=(x-2)²+6ですね。

よって、この二次関数の頂点の座標は(2,6)です。

※二次関数の頂点について深く学習したい人は、二次関数の頂点について詳しく解説した記事をご覧ください。

この頂点の座標をx軸方向に3、y軸方向に-5移動させると、点(5,1)になりますね。

頂点が点(2,6)から(5,1)に移動したので、

求める二次関数は

y=(x-5)²+1

となります。以上が、平方完成を利用して二次関数を平行移動させる方法です。

 

平行移動の解き方：その２

二次関数のグラフを平行移動させる方法の２つ目を紹介します。

今回は、平方完成は使いません。

先ほどと同様に、y=x²-4x+10という二次関数のグラフを、x軸方向に3、y軸方向に-5平行移動させる場合を考えてみます。

この時、xを(x-3)に、yを{y-(-5)}に置き換えることで、平行移動後の二次関数のグラフを求めることができます。

{(y-(-5)}=(x-3)²-4(x-3)+10

より、

y+5

= (x²-6x+9)-4x+12+10

=x²-10x+31

となるので、左辺の5を右辺に移動して、

y=x²-10x+26

となり、平方完成して平行移動させた場合と同じ二次関数が得られました。

 

二次関数のグラフを平行移動させる解き方の解説は以上です。

 

３：二次関数グラフの頂点の公式

最後に、二次関数のグラフの頂点と軸を一発で求めることができる公式を紹介します。

知っておくと非常に便利なので、ぜひ覚えておきましょう。

y=ax²+bx+cという二次関数のグラフがある時、このグラフの頂点の座標は以下のようになります。

以上の公式を知っていれば、わざわざ二次関数を平方完成しなくても頂点の座標を求めることができます。

※なぜ以上の公式が成り立つのかを学習したい人は、二次関数の頂点について詳しく解説した記事をご覧ください。

例として、二次関数y=2x²+8x+10のグラフの頂点の座標を、以上の公式を使って求めてみます。

まず、

頂点のx座標

= -(8/2・2)

= -2

ですね。

頂点のy座標

= -(8²-4・2・10/4・2)

= -(16/8)

= -2

です。

したがって、二次関数y=2x²+8x+10のグラフの頂点の座標は、（-2,-2）となります。

 

二次関数グラフの書き方＆頂点のまとめ

二次関数グラフに関する解説はこれで終わりです。

二次関数のグラフは、数学の分野の中でも非常に基礎的な事柄の１つです。

忘れてしまった場合は、またこの記事で復習をして、二次関数のグラフの書き方を思い出してください。

理系科目だけに力を注いでいませんか？
10万人近くもの高校生が読んでいる読売中高生新聞を購読して国語・社会・英語の知識もまとめて身につけましょう！購読のお申し込みはここをクリック！

 

この記事の執筆者

ニックネーム：やっすん

早稲田大学商学部4年
得意科目：数学