変化の割合&傾きの求め方！二次関数のポイントを即理解しよう！

中学数学・高校数学における変化の割合とは何か、変化の割合の求め方・公式について早稲田大生がわかりやすく解説します。

一次関数における変化の割合は、一次関数の傾きに等しくなり、変化の割合はyの増加量÷xの増加量で求めることができます。（後に詳しく解説します）

本記事では、一次関数における変化の割合だけでなく、二次関数における変化の割合についても解説している充実の内容です。

最後には、変化の割合に関する計算問題も用意しました。

ぜひ最後まで読んで、変化の割合とは何か、変化の割合の求め方・公式を理解してください！

【PR】勉強を効率的に継続して、志望校に合格したい方必見！

↓無料ダウンロードはこちら↓

1：変化の割合とは？

まずは変化の割合とは何かについて解説します。

変化の割合とは、ある関数（一次関数y=ax+bや二次関数y=ax²+bx+c）においてxの値がαだけ増加した時に、yの値がβだけ増加したとすると、β /α（yの増加量 / xの増加量）のことを変化の割合と言います。

以上が変化の割合の定義になります。

しかし、これだけではさすがにわかりにくいので、次の章からは具体例で変化の割合の求め方・公式を解説していきます。

2：変化の割合の求め方・公式

では、具体的な関数（一次関数）で変化の割合の求め方・公式を見ていきます。

※一次関数があまり理解できていない人は、一次関数について詳しく解説した記事をご覧ください。

変化の割合：具体例１

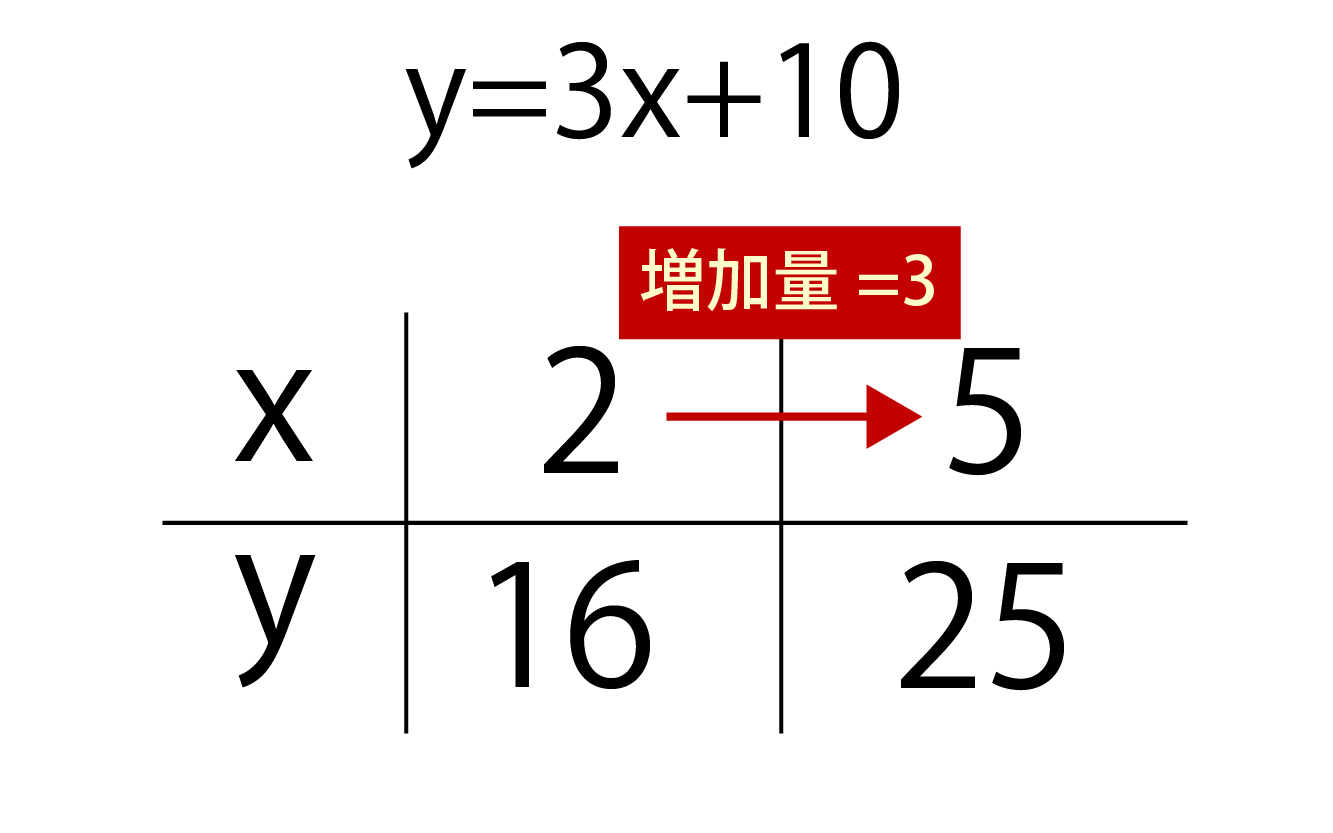
例えば、y=3x+10という一次関数があるとします。

この時、xの値が2から5に増加したとします。

すると、yの値はどのように変化するでしょうか？

x=2の時、

y=3・2+10=16ですね。

x=5の時、

y=3・5+10=25ですね。

よって、yの値は16から25になっているので、yの増加量は

25-16=9

となります。

変化の割合は「yの増加量 / xの増加量」で求められるので、

y=3x+10の変化の割合は

9（yの増加量）/ 3（xの増加量）

=3・・・（答）

となります。

※xの値は2から5に変化しているので、xの増加量は3です。

変化の割合の求め方が理解できましたか？では、もう一つ、変化の割合を求める具体例を見てみましょう。

変化の割合：具体例２

y=-2x-5という一次関数において、
Xの値が-5から-7に変化した時の変化の割合を求めてみます。
まず、xの値が-5から-7に変化しているので、xの増加量は
-7-(-5)=-2ですね。
X=-5の時、
Y=(-2)・(-5)-5=5
x=-7の時、
y =(-2)・(-7)-5=9です。

なので、yの増加量は
9-5=4ですね。
したがって、変化の割合は、
4（yの増加量）/ -2（xの増加量）
=-2・・・（答）
となります。
変化の割合の求め方が理解できましたか？

3：一次関数における変化の割合は傾きに等しい

以上で変化の割合を求めてみて、気づいたことはありませんか？

一次関数y=3x+10の変化の割合は3でした。

一次関数y=-2x-5の変化の割合は-2でした。

一次関数の傾きが変化の割合になっていることに気づきましたか？

これは偶然ではありません。

一次関数における変化の割合は、一次関数の傾きに等しくなります。

これはとても重要なので、必ず覚えておきましょう！

一次関数における変化の割合=傾きになる理由

では、なぜ一次関数における変化の割合は傾きに等しくなるのでしょうか？

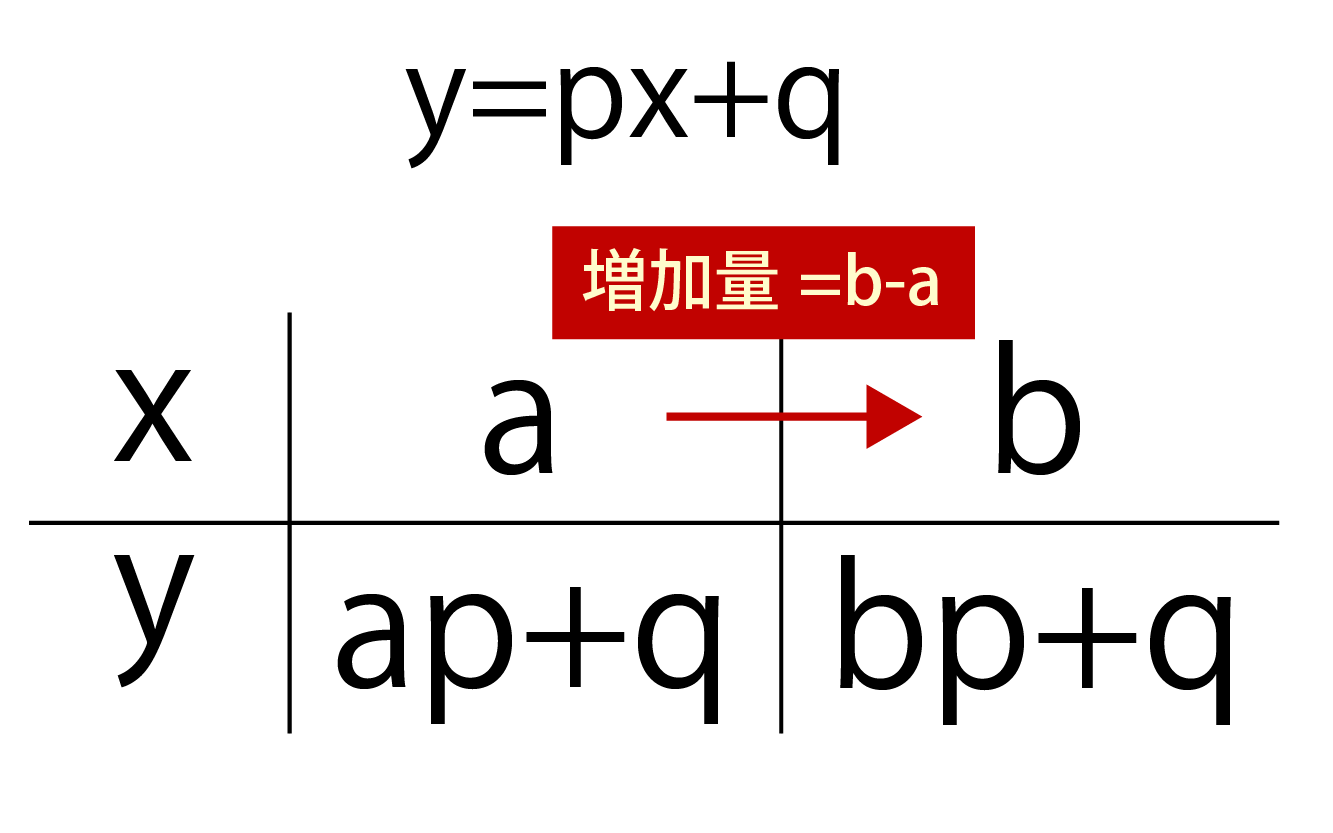
例えば、y=px+qという一次関数があったとします。

この時、xの値がaからbに変化したとします。

すると、xの増加量はb-aですね。

x=aの時、

y=ap+q

x=bの時、

y=bp+q　です。

よって、yの増加量は

(bp+q)-(ap+q)

=(b-a)p　ですね。

したがって、変化の割合は

{(b-a)p} / b-a

= p　となり、

一次関数y=px+qの傾きpに等しくなります。

以上が一次関数における変化の割合=傾きになる理由（証明）です。

4：二次関数における変化の割合を求めてみよう！

先ほどまでは一次関数の変化の割合を求めてきました。

今度は二次関数の変化の割合を求めてみましょう！

※二次関数があまり理解できていない人は、二次関数について詳しく解説した記事をご覧ください。

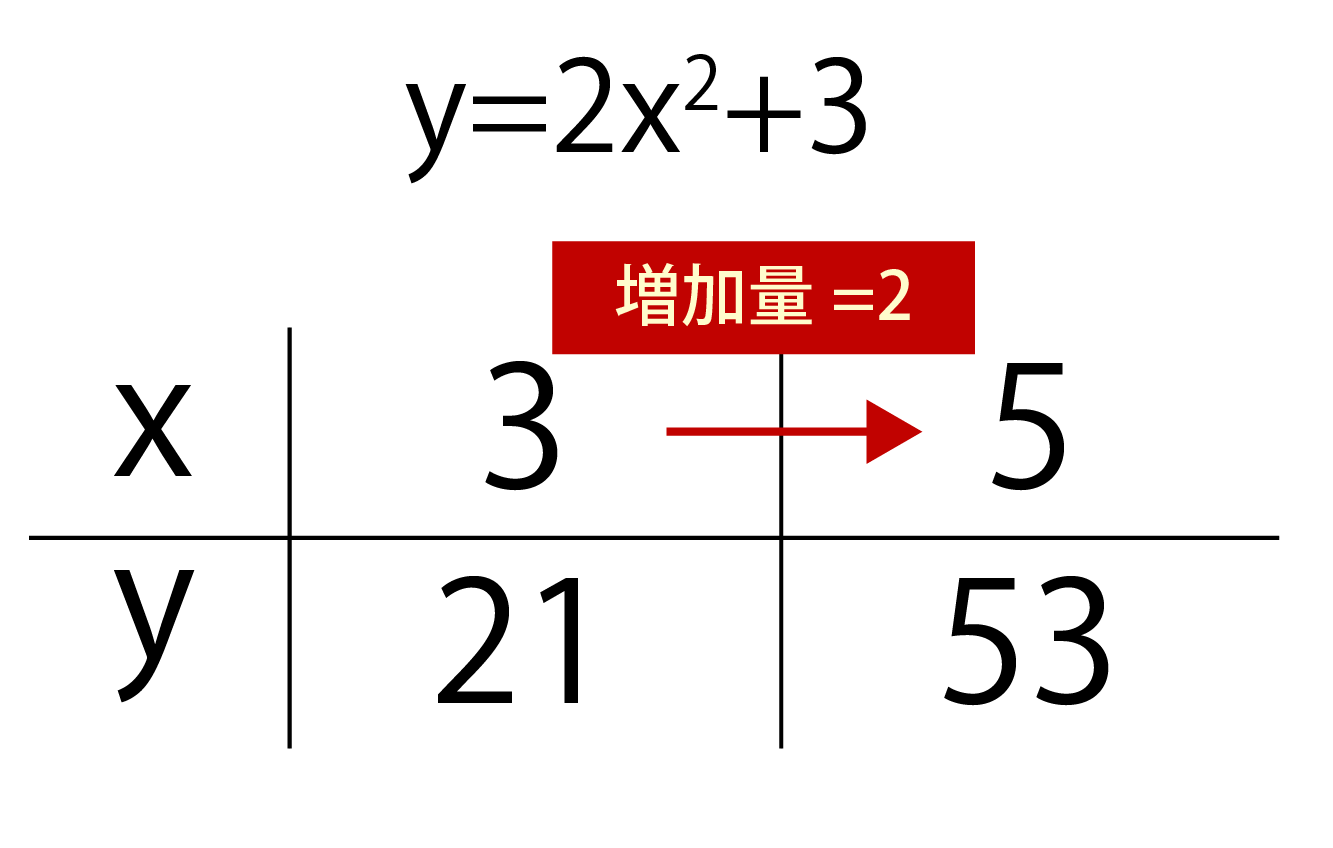
二次関数y=2x²+3があるとします。

xの値が3から5に変化したとします。

すると、xの増加量は

5-3=2ですね。

x=3の時、

y=2・3²+3=21

x=5の時、

y=2・5²+3=53ですね。

よって、yの増加量は

53-21=32です。

したがって、変化の割合は

32 / 2 = 16・・・（答）

となります。

変化の割合の求め方はの手順は一次関数の時と同じですね。

二次関数の場合、変化の割合はy=ax²+bのaと等しくはならないので注意しましょう！

5：変化の割合に関する計算問題

最後に、変化の割合に関する計算問題をいくつか解いてみましょう。

詳しい解答＆解説付きなので安心して解いてください。

計算問題１

一次関数y=5x+6において、xの値が20から30に変化した。

この時、yの値の増加量を求めよ。

解答＆解説

まず、一次関数がy=5x+6なので、変化の割合は5（変化の割合=傾きでした）で一定です。

xの値は20から30に変化しているので、xの増加量は10です。

したがって、

5（変化の割合）

= （yの増加量）/ 10（xの増加量）

なので、

yの増加量

= 50・・・（答）

となります。

計算問題２

yはxの一次関数で、変化の割合は5である。

x=2の時、y=40である時、この一次関数の式を求めよ。

解答＆解説

一次関数の変化の割合が5なので、求める一次関数は

y=5x+b　と表現できますね。

x=2の時、y=40なので、

40=5・2+bより、

b=30です。

したがって、求める一次関数の式は

y=5x+30・・・（答）

となります。

まとめ

変化の割合が理解できましたか？

一次関数において、変化の割合=傾きとなることは必ず覚えておきましょう。

変化の割合を忘れてしまった時は、また本記事で変化の割合を復習しましょう！