三倍角の公式の覚え方・ゴロ合わせ！証明＆問題付き

高校数学の三角関数における、三倍角の公式について解説します。

数学が苦手な人でも三倍角の公式がマスターできるように、現役の早稲田大生が解説します。

本記事を読めば、三倍角の公式と覚え方（ゴロ合わせ）・三倍角の公式の証明が理解できます！

最後には、三倍角の公式を使った練習問題も用意した充実の内容です。

ぜひ最後まで読んで、三倍角の公式をマスターしてください。

 

三角関数の公式の理解に役立つ記事のまとめもぜひ参考にしてみてください！

 

１：三倍角の公式の覚え方（ゴロ合わせ）

まずは三倍角の公式を暗記しましょう！

三倍角の公式は、三角関数の分野で暗記すべき項目の１つです。必ず暗記しておきましょう。

三倍角の公式の覚え方（ゴロ合わせ）も用意したので、三倍角の公式が覚えやすくなっているかと思います。

【三倍角の公式：覚え方（ゴロ合わせ）】

● sin3θ=3sinθ – 4sin³θ

・覚え方（ゴロ合わせ）

→「サインさんは、山菜から３つの余震感じる」

● cos3θ=4cos³θ – 3cosθ

・覚え方

→cos3θの公式は、sin3θの公式の右辺において、符号を逆にして、sinをcosに変換するだけです。

三倍角の公式の覚え方（ゴロ合わせ）は以上になります。

繰り返しになりますが、三倍角の公式は三角関数の分野では暗記必須です。必ず暗記しておきましょう。

 

２：三倍角の公式の証明

なぜ三倍角の公式は成り立つのでしょうか？本章では、三倍角の公式の証明を解説します。

まずはsin3θの証明から解説します。

三倍角の公式：証明（sin3θ）

3θ=2θ+θであることに注目します。

sin3θ

=sin(2θ+θ) ・・・①

ですね。ここで、加法定理を使います。

※加法定理が理解できていない人は、加法定理について解説した記事をご覧ください。

加法定理より、

①

=sin2θcosθ+cos2θsinθ・・・②

ここで、二倍角の公式を使います。

※二倍角の公式が理解できていない人は、二倍角の公式について解説した記事をご覧ください。

二倍角の公式より、

②

=2sinθcosθ・cosθ+(1-2sin²θ)・sinθ

=2sinθcos²θ+sinθ-2sin³θ

=2sinθ(1-sin²θ)+sinθ-2sin³θ

=-4sin3θ+3sinθ

以上で、三倍角の公式（sin3θ）が証明できました。

 

三倍角の公式：証明（cos3θ）

cos3θの証明も、3θ=2θ+θに注目します。

cos3θ

=cos(2θ+θ)・・・③

ここで、加法定理を使います。

※加法定理が理解できていない人は、加法定理について解説した記事をご覧ください。

③

=cos2θcosθ-sin2θsinθ・・・④

ここで、二倍角の公式を使います。

※二倍角の公式が理解できていない人は、二倍角の公式について解説した記事をご覧ください。

④

=(2cos²θ-1)・cosθ-2sinθcosθ・sinθ

=2cos³θ-cosθ-2sin²θcosθ

=2cos³θ-cosθ-2(1-cos²θ)cosθ

=4cos³θ-3cosθ

以上が三倍角の公式（cos3θ）の証明です。

三倍角の公式の証明は、加法定理と二倍角の公式を組み合わせで行うことを覚えておきましょう！

 

３：三倍角の公式を使った練習問題

最後に、三倍角の公式を使った練習問題を解いてみましょう。

どんな場面で三倍角の公式を使うのか？がイメージできると思います。

三倍角の公式：練習問題

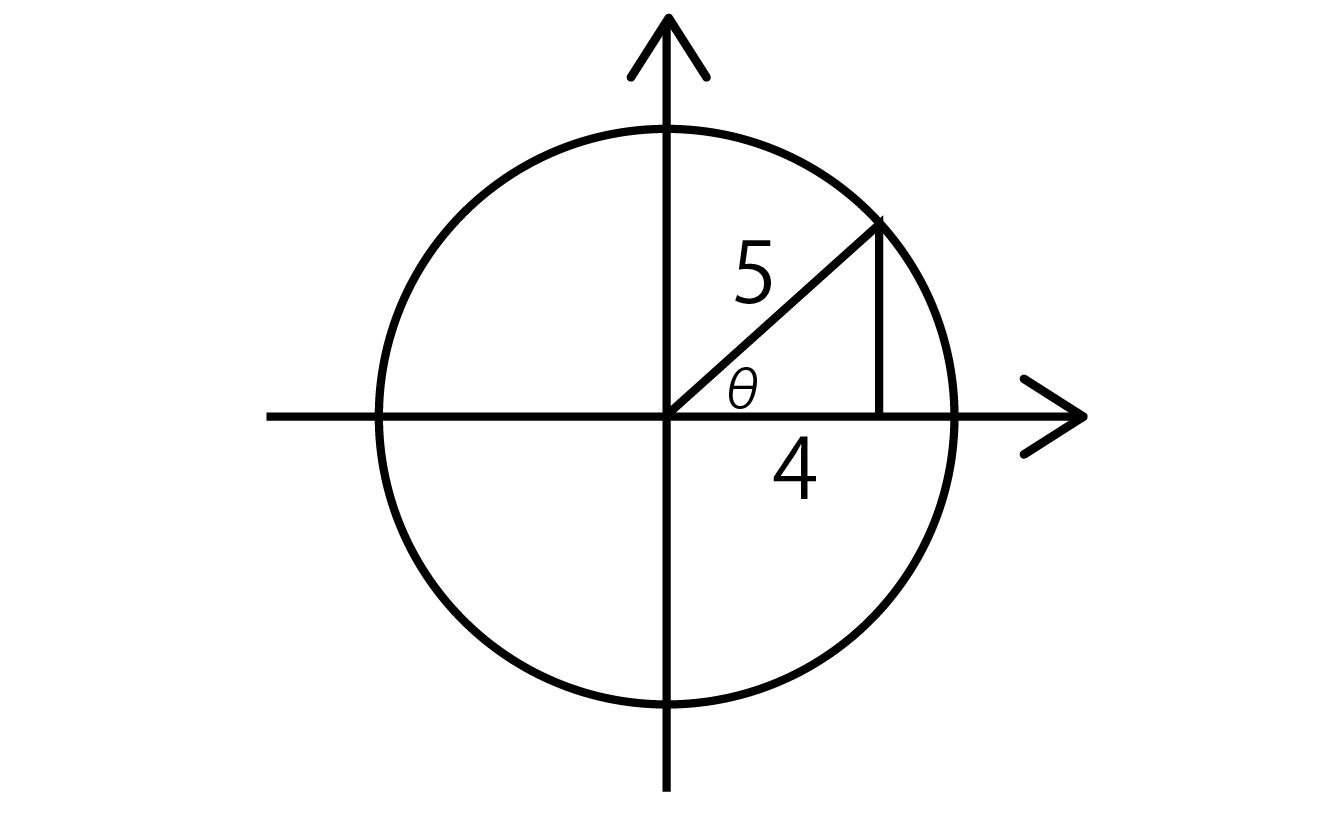
θが第一象限の角で、cosθ=4/5の三角形がある。

このとき、sin3θとcos3θの値を求めよ。

解答＆解説

まず、θが第一象限の角で、cosθ=4/5の三角形は以下のようになりますね。

よって、sinθ=3/5となります。（3：4：5の三角形ですね。）

したがって、三倍角の公式より、

sin3θ

=3・(3/5)- 4・(3/5)³

=117/125・・・（答）

また、同様に三倍角の公式より、

cos3θ

=4・(4/5)³-3・(4/5)

=-44/125・・・（答）

 

三倍角の公式のまとめ

いかがでしたか？

三倍角の公式の覚え方（ゴロ合わせ）・三倍角の公式の証明の解説は以上になります。

繰り返しになりますが、三倍角の公式は三角関数の分野でも暗記必須の事柄の１つです。

三倍角の公式を忘れたときは、また本記事で三倍角の公式を思い出しましょう！

この記事の執筆者

ニックネーム：やっすん

早稲田大学商学部4年
得意科目：数学