二倍角の公式の覚え方はこれ！即覚えられる語呂合わせを紹介！

三角関数の問題は入試問題でよく出てくるのに、二倍角の公式がどうしても覚えられない方が多いと思います。

本記事では、sin2θ,cos2θ, tan2θなどの高校数学の三角関数における二倍角の公式を、語呂合わせを使用して解説します。

また、三角関数の二倍角の公式の一覧・二倍角の公式の覚え方（語呂合わせ）・二倍角の公式の証明・二倍角の公式を使った練習問題で定着させましょう。

数学が苦手な人でも理解できるように二倍角の公式について丁寧に解説しているので、ぜひ最後まで読んで、二倍角の公式をマスターしてください。
詳しくは「▶︎三角関数の公式の理解に役立つ記事のまとめ」もぜひ参考にしてみてください！

		
【PR】勉強を効率的に継続して、志望校に合格したい方必見！

↓無料ダウンロードはこちら↓

二倍角の公式の覚え方（語呂合わせ）

まずは二倍角の公式の一覧と二倍角の公式の覚え方（語呂合わせ）を紹介します。

二倍角の公式は、三角関数の分野でもかなり重要なので、必ず暗記しましょう！（二倍角の公式の証明については次の章で解説します。）

二倍角の公式一覧・覚え方（語呂合わせ）

sin2θ = 2sinθcosθの語呂合わせ：sinは錦織

・覚え方（語呂合わせ）

→「sinは錦織！」

cos2θ＝ 2cos²θ- 1は「コス兄は２人のコス爺より低い」

= cos²θ- sin²θ

= 1- 2sin²θ

= 2cos²θ- 1

tan2θ= 2tanθ/（1- tan²θ）は「一匹タンタン、２つのタン」

= 2tanθ/（1- tan²θ）

・覚え方（語呂合わせ）

→「一匹タンタン、２つのタン」

以上が二倍角の公式一覧と、二倍角の公式の覚え方（語呂合わせ）です。

繰り返しになりますが、二倍角の公式は三角関数の分野では頻出なので必ず暗記してください！

二倍角の公式の証明

では、なぜ二倍角の公式は成り立つのでしょうか？本章では、二倍角の公式が成り立つ理由（二倍角の公式の証明）を行います。

二倍角の公式：証明（sin2θ）

二倍角の公式の証明は、加法定理を使えば簡単にできます。

※加法定理を忘れた人は、詳しくは「▶︎加法定理とは？公式と証明、簡単な覚え方を語呂合わせで説明します！」をご覧ください。

sin2θ

=sin(θ+θ)

=sinθcosθ+sinθcosθ

=2sinθcosθ

以上でsin2θの二倍角の公式の証明ができました。

二倍角の公式：証明（cos2θ）

cos2θの二倍角の公式の証明も加法定理を使います。

※加法定理を忘れた人は、詳しくは「▶︎加法定理とは？公式と証明、簡単な覚え方を語呂合わせで説明します！」をご覧ください。
cos2θ

=cos(θ+θ)

=cosθcosθ-sinθsinθ

=cos²θ-sin²θ・・・（※1）

ですね。ここで、

sin²θ+cos²θ=1・・・（※2）でした。よって、

cos²θ=1-sin²θ なので、これを（※1）に代入して、

cos2θ=1-2sin²θ

また、（※2）より、

sin²θ=1-cos²θ なので、これを（※1）に代入して

cos2θ=2cos²θ-1

となります。cos2θの二倍角の公式の証明は以上です。

二倍角の公式：証明（tan2θ）

tan2θの二倍角の公式の証明も加法定理を使います。

※加法定理を忘れた人は、詳しくは「▶︎加法定理とは？公式と証明、簡単な覚え方を語呂合わせで説明します！」をご覧ください。

tan2θ

=tan(θ+θ)

=（tanθ+tanθ）/（1-tanθtanθ）

=2tanθ/（1-tan²θ）

簡単ですよね？tan2θの二倍角の公式の証明は以上です。

二倍角の公式の証明は、どれも加法定理を使えば良いことがわかったと思います。二倍角の公式は、忘れてしまっても導出できるように、加法定理もしっかり覚えておきましょう！

二倍角の公式のを使った練習問題

最後に、三角関数の二倍角の公式を使った練習問題を解いてみましょう。実際の問題では、二倍角の公式をどのように使うのかがイメージできるでしょう。

二倍角の公式：練習問題

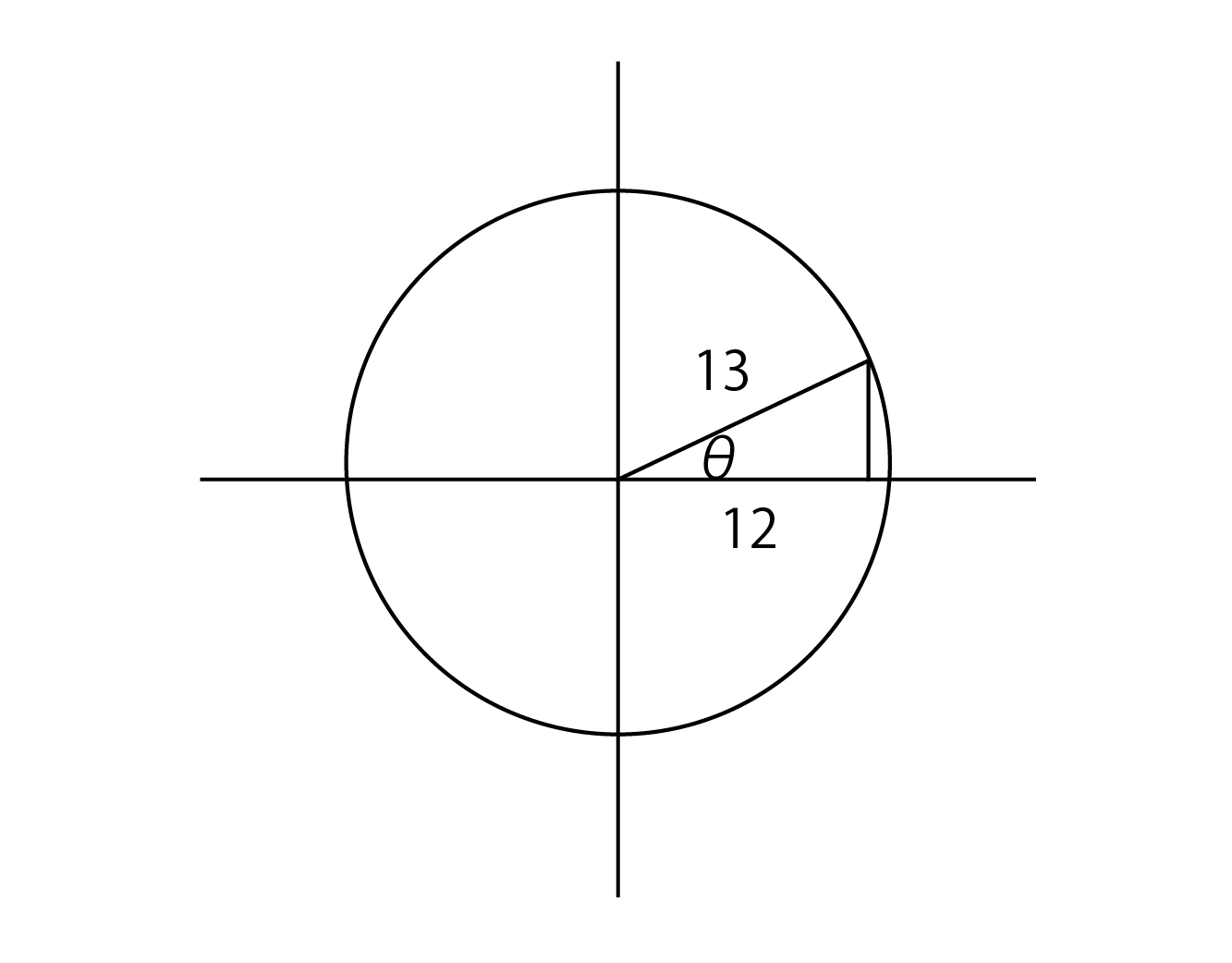
θが第一象限の角で、cosθ=12/13の三角形がある。

この時、sin2θ、cos2θ、tan2θの値を求めよ。

解答＆解説

まず、θが第一象限の角で、cosθ=12/13の三角形は、図にすると以下のようになりますね。

まずはsinθを求めましょう。cosθ=12/13より、sinθ=5/13ですね。

（5:12:13の三角形です。）

よって、二倍角の公式より、

sin2θ

=2・5/13・12/13

=120/169・・・（答）

となります。

次はcos2θを求めます。

cosθの求め方は３つありましたが、今回はcos2θ=1-2sin²θを使ってみます。

cos2θ

=1 – 2・（5/13）²

= 119/169・・・（答）

※cos2θ=2cos²θ-1を使ってみると、

cos2θ

=2・（12/13）² – 1

= 119/169

より、上記と同じ結果になりますね。

最後に、tan2θを求めます。

tan2θの二倍角の公式を使って求めても良いのですが、

tanθ=sinθ/cosθ

であることを思い出してください。

これを使えば、

tan2θ

= sin2θ/cos2θ

= （120/169）/（119/169）

= 120/119・・・（答）

となります。

tan2θは、sin2θとcos2θがわかればそこから楽に求めることができますね。

二倍角の公式：まとめ

以下がでしたか？二倍角の公式の覚え方（語呂合わせ）・二倍角の公式の証明・二倍角の公式の練習問題は以上です。

繰り返しになりますが、二倍角の公式は三角関数の中でも非常によく使うので、必ず覚えましょう！

二倍角の公式を忘れた時は、加法定理から二倍角の公式を導きましょう！

受験生の勉強に役立つLINEスタンプ発売中！

最新情報を受け取ろう！

受験のミカタから最新の受験情報を配信中！