シャルルの法則とは？身近な例で徹底解説！豆知識付き

今回はシャルルの法則を物理が苦手な人でも理解できるように丁寧に解説します。

シャルルの法則は、ボイルの法則と並んで頻繁に問題に出題されます。

※ボイルの法則について詳しく学習したい人は、ボイルの法則とは？身近な例で丁寧に解説＆豆知識付きをお読みください。

今回は、皆さんにシャルルの法則を理解して頂くため、身近な例とスマホでも見やすい図を用いて解説しました。

また、シャルルの法則が本当に理解できたかを試すのに最適な練習問題や知っていると鼻が高くなるシャルルの法則の豆知識も紹介しています。

この記事を読めばもうシャルルの法則は完璧でしょう。ぜひ最後までお読みください。

【PR】勉強を効率的に継続して、志望校に合格したい方必見！

↓無料ダウンロードはこちら↓

１．シャルルの法則：公式

まずは、シャルルの法則とは何なのかとシャルルの法則の公式を紹介します。

シャルルの法則とは、定圧変化させた時に生じる体積と絶対温度の関係を示した式（公式）のことです。

※定圧変化＝気体の圧力を一定に保って温度や体積を変化させること

※絶対温度＝理論的に分子の熱運動がなくなる温度(マイナス273℃)を0[K:ケルビン]とする温度のこと。私たちが普段使っている温度の単位(℃)はセルシウス度と言います。このセルシウス度(t[℃]とする)に273を足したものが絶対温度(T[K]とする)です。

T[K] = 273 + t[℃]

とある容器に気体を入れて、気体の圧力を一定に保ちながら加熱し、圧縮・膨張させると、気体の体積V[m³]は絶対温度T[K]に比例し、V/T = K(一定)の関係が成り立ちます。

これをシャルルの法則といいます。

シャルルの法則

V / T = K(一定)

(V[m3]：体積、T[K]：絶対温度)

以上がシャルルの法則に関する基本的な事柄ですが、これだけだと分かりにくいので、身近な例でさらに詳しく解説していきます。

２．シャルルの法則：身近な例

身近な例でシャルルの法則をさらに深く理解していきましょう。

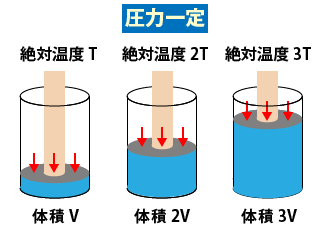
以下のイラストのように、筒（シリンダーといいます）の中に気体を入れて、圧力を一定に保ちながら加熱して体積を膨張させていきます。

イラストにすると、シャルルの法則のイメージがわきやすくなったのではないでしょうか？

気体を加熱すると、体積は膨張します。この温度（絶対温度）と体積の関係を表したものがシャルルの法則というわけですね。

体積 ÷ 絶対温度は常に一定ということを必ず頭に入れておきましょう！

３．シャルルの法則：問題

では、ここでシャルルの法則に関する問題を１つ解いてみましょう。
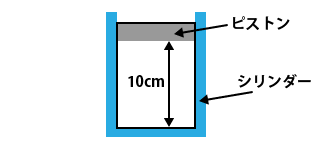
[シャルルの法則：問題]
下図のように、シリンダーの中に7℃の空気が入っている。ピストンの面積は60cm²で動くようになっている。最初のピストンはシリンダーの底から10cmの高さにあった。シリンダーを熱して温度を27℃にすると、ピストンは何cm上昇するか。

[解答＆解説]

シリンダー内の空気の圧力は、常に大気圧とピストンの重さによる圧力の話に等しいので、定圧変化です。よって、シャルルの法則が成り立ちます。

ピストンが上昇する高さをx[cm]とおく。シャルルの法則より、

(60×10) / (273+7)

＝ 60×(10+x) / (273+27)

これを解いて

x=0.71[cm]・・・(答)

シャルルの法則では、必ず絶対温度を使用することに気をつけましょう。

４．シャルルの法則：豆知識

最後に、シャルルの法則に関する豆知識を１つ紹介します。

シャルルの法則と絶対温度に関する事柄です。

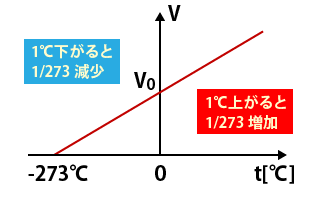
・シャルルさんは、圧力一定のもとで気体を熱すると、すべての気体が、温度が1度上昇するごとに、0℃の時の体積V₀の1/273ずつ増加することを発見しました。（←偉大！）

・これをグラフにすると、以下のようになります。このグラフを左に延長すると、ー1℃で気体の体積は272/273V₀、ー2℃で271/273V₀、ー273℃で0になる。ー273℃を0Kとする絶対温度はここから生み出されました！

いかがでしたか？シャルルの法則が理解できましたか？

シャルルの法則は物理の中でも頻繁に出題される分野の１つです。シャルルの法則を忘れた時はこの記事を読み返してまた思い出してください！