三角関数とは？三角関数の基礎、試験にでる要点まとめ

三角関数は大学入試で頻出の範囲の一つです。

センター試験でもここ５年間で2011年、2013年、2015年と２年に１度のペースで出題されています。

また、2015年度は早稲田大学で3学部（国際教養、人間科学、社会科学部）、慶応大学で５学部（理工、経済、環境情報、看護、薬学部）で三角関数に関する問題が出題されました。

このように入試で出題頻度の高い三角関数ですが、覚える公式が多くて、多くの受験生が苦労している分野です。

だから、場当たり的に覚えるのではなくまとめていっぺんに覚えてしまう方が効率がよいです。

そこで、今回は、三角関数の公式や性質など入試に出やすい重要な部分に絞り、要点をまとめました。

是非、三角関数をおさらいしてみてください！

三角関数の基本的な理解に役立つ記事のまとめもぜひ参考にしてみてください！

1. 三角関数　定義&大事な性質

この章では三角関数の定義や三角関数のグラフ、性質を紹介します。

1-1. 三角関数って何？

三角関数を勉強する上で「sin（サイン）」や「cos（コサイン）」とは何か？を理解しなくては成りません。

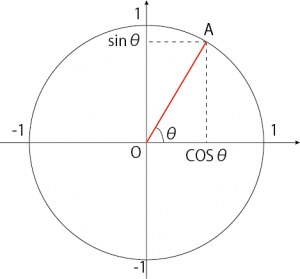
これら２つを定義するには下図のような単位円が必要になります。

ちなみに単位円とは、１辺の長さが１の円のことをいいます。

上図においてAのXの値をcosθ、Yの値をsinθと定義します。

つまり・・

になります。tanθは傾きを示します。

ちなみに、単位円以外の半径がRの円では・・

と定義する事が出来ます。

1-2. 三角関数　必ず覚えなくてはならない3つの性質

三角関数には大事な性質が3つあります。この3つは三角関数の式を変換していく上で欠かせません。必ず暗記しましょう。

①sin^２θ+cos^２θ=1

②

③

証明や詳しい解説は『三角関数の基礎　必ず覚えておかなくてはならない5つの性質』をご覧ください。

1-3. 三角関数　グラフ&θの変動

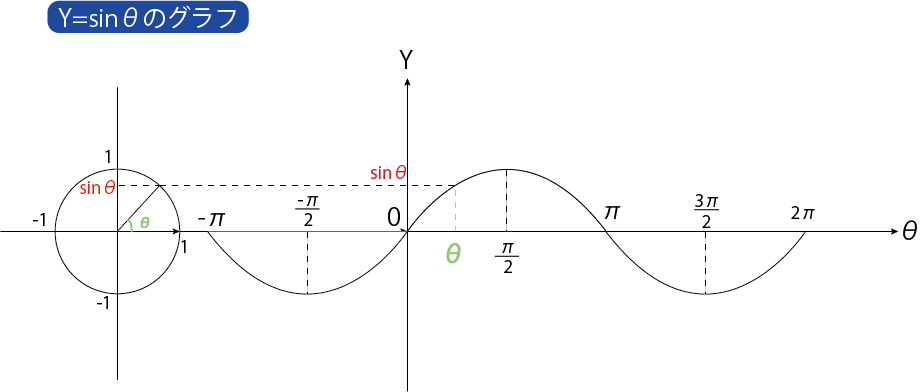
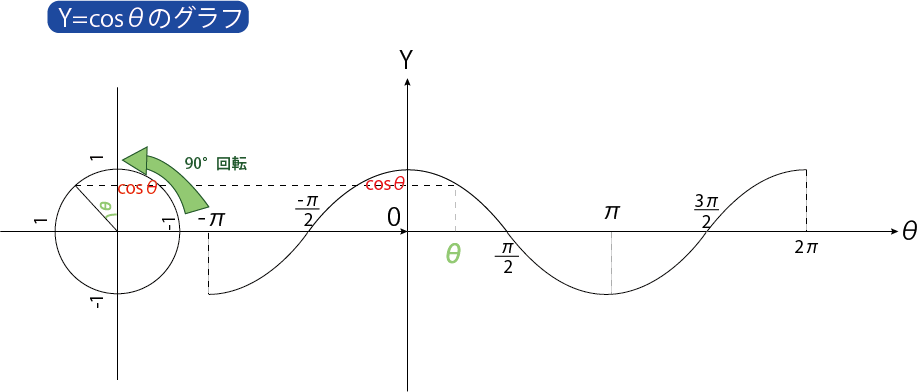
Y=sinθやY=cosθはθの値によってYの値が変動します。例えば、→のように変動するのは分かりますよね。このような変化をプロットしたものが以下の３つのグラフになります。

これらのグラフは自分で書ける事が大事なので書けるようになるまで練習してください。

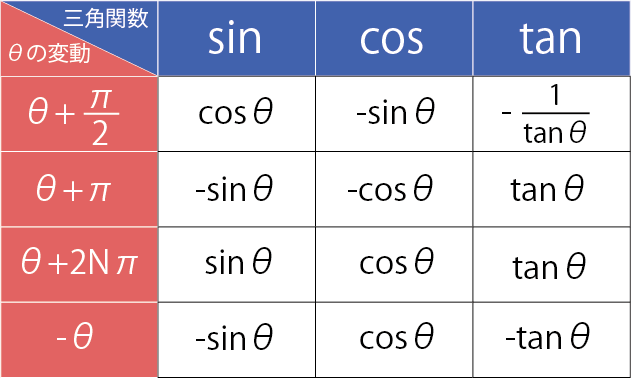
また、θにを足したり、−にしたりする事でsinやcosの値が変化します。受験問題では、式の過程でsin→cosにしたりする時に使われるので、これも頭に入れておく事が必要です。

グラフと照らし合わせる事で理解が深まりますのでY=sinθやY=cosθのグラフと照らし合わせて覚えていってください！

詳しい解説・証明は『三角関数の基礎　必ず覚えておかなくてはならない5つの性質』をご覧ください。

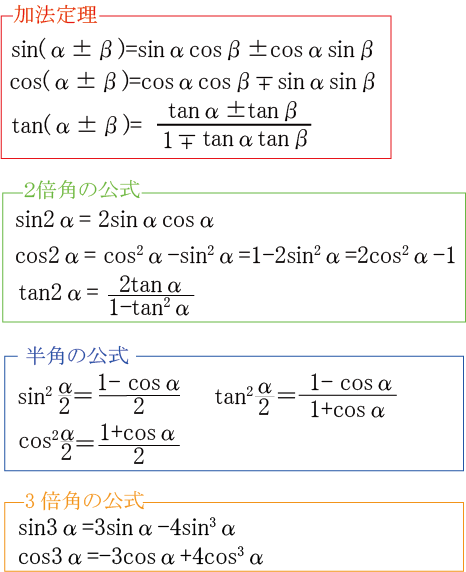
2. 三角関数　加法定理

三角関数の範囲で必ず覚えなくては成らない公式が一つあります。それが・・加法定理です！

この中で必ず覚えなくてはならないのが上記赤枠で囲った加法定理です。最悪、２倍角や3倍角、加法定理から作り出す事が出来ます。（くわしくは「三角関数の基礎2　加法定理　公式・証明・覚え方」を参照してください）

ただ、2sinαcosαからsin2αの変換など、式を見ただけで式を簡易化しなくてはならないケースがあるので、２倍角、3倍角、半角も覚えるようにしましょう。

以前、東京大学でも出題した加法定理の証明や問題など加法定理の詳細をまとめたものが「三角関数の基礎2　加法定理　公式・証明・覚え方」に書かれているので、加法定理を詳しく勉強したい方は以下をご覧ください。

3. 三角関数　積和の公式　和積の公式

積和の公式・和積の公式は覚えているだけで、格段に解くスピードが速くなる場合があります。

積和の公式も和積の公式も、もちろん、加法定理から導きだす事が出来ます。よく「和積も積和も覚える必要がない！」と断言する人がいます。しかし、和積・積和を使わないと早く解けない問題があります。それが以下の問題です。

解説はこちら！

積和&和積の公式の証明は「三角関数の基礎3　積和の公式&和積の公式」に書かれておりますので、一から積和や和積を勉強したい方は目を通しておいてください！

4. 三角関数　合成

三角関数の中で、受験生がもっとも苦労する分野が三角関数の合成です。

まずは、合成の式です。これは必ず覚えてください。

三角関数の合成の公式は分かるけど、どの場面で使えばいいか分からない人もいるのではないでしょうか？合成がよく使われる場面は以下の２つになります。

①方程式、不等式を解く場合

②最小値、最大値を求める場合（こちらが圧倒的に多いです。）

理由は・・

三角関数を合成する事で、今までsinとcosを同時に使っていた方程式をsinのみの方程式に変換出来るからです。つまり変数を一つにする事で、関数の動向が見やすくなります。だから、最小値、最大値を求めやすくなります。

最後に一つ問題を出します。少し難易度が高いですが、これまで勉強した事を駆使すれば解けない問題ではありません。

【応用】早稲田国際教養（類題）

4cos^２θ+2sin^２θ+2sinθcosθの最大値・最小値を求めなさい。

この問題の解説はこちらです。

三角関数　合成の証明や具体的な使い方などもっと詳しく勉強したい方は「三角関数の基礎4　三角関数の合成のコツ」をご覧ください。

以上の公式や性質を丁寧に覚えれば、三角関数の問題で以前よりもつまづく事はなくなるでしょう。実践を通じてどのような場面でその公式が使われるのかを身につけていってください！