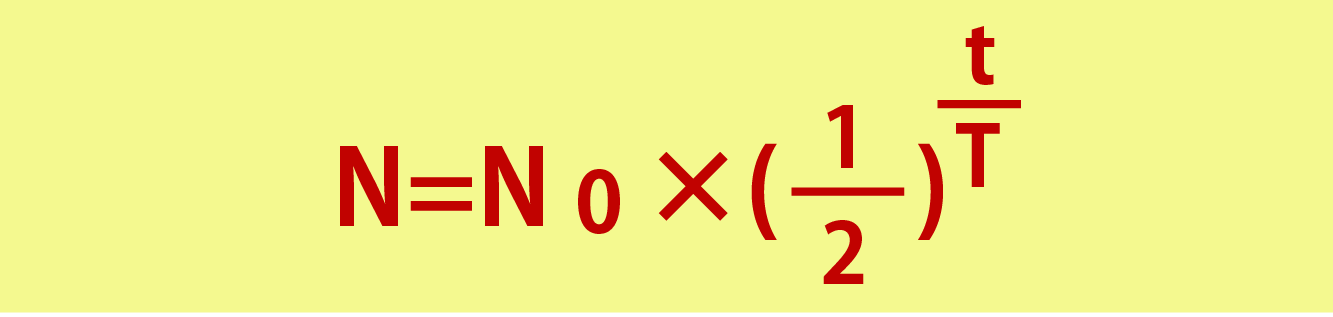半減期とは？これで半減期の公式と計算方法が必ずわかる！

半減期について、物理が苦手な人にもわかるように、スマホでも見やすい図を用いて解説していきます。

本記事では、半減期とは何か？という説明に加えて、半減期の計算方法についても解説しています。

最後には、半減期についての理解を確認するために半減期の計算問題もご用意しました。ぜひ最後まで読んで、半減期をマスターしてください。

		
【PR】勉強を効率的に継続して、志望校に合格したい方必見！

↓無料ダウンロードはこちら↓

１：半減期とは？

半減期とは何かについて解説していきます。

まず、原子番号83のビスマスまでの原子核は比較的安定しているのですが、原子番号84以上の原子核は不安定になるという事実があります。

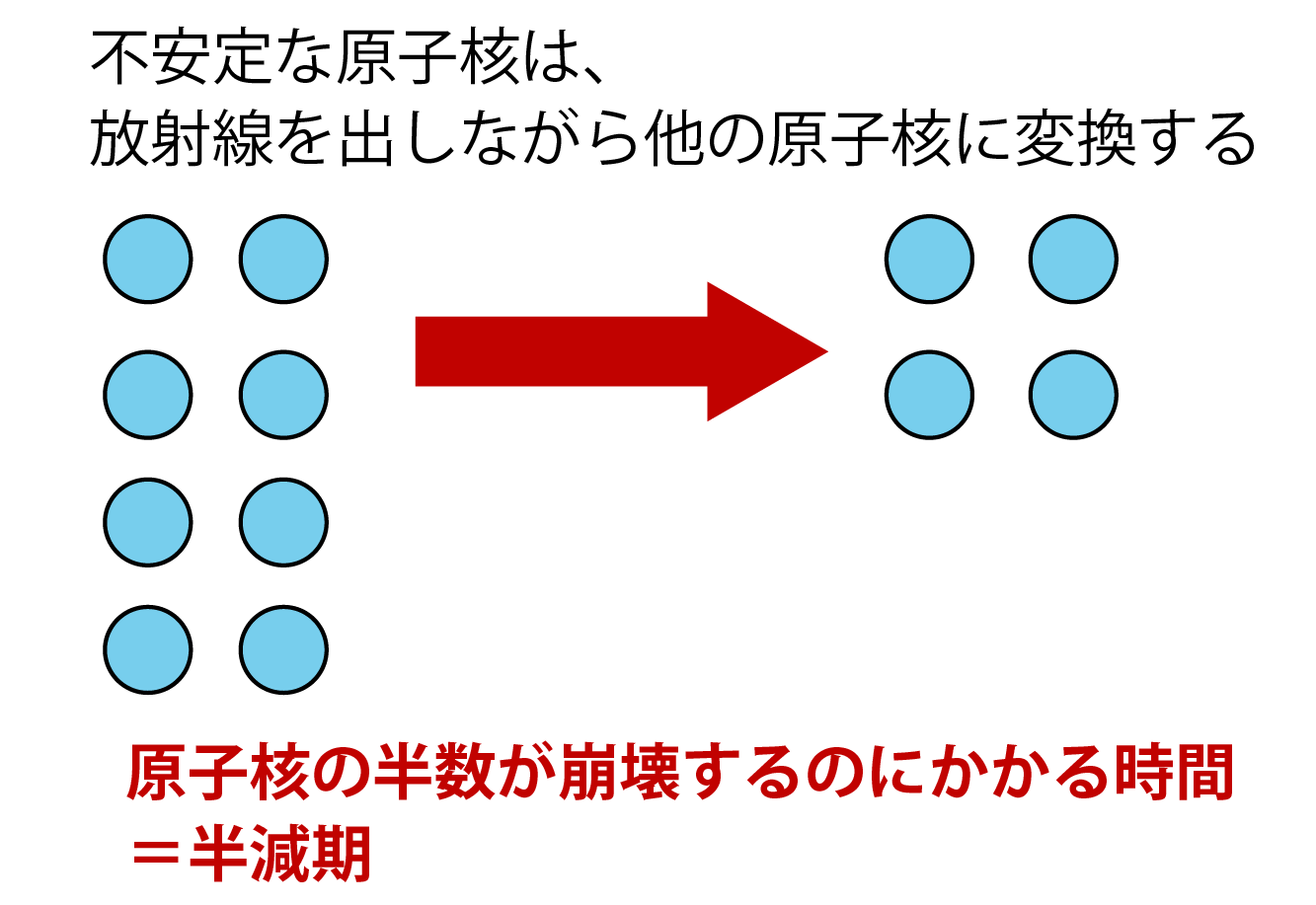
もちろん不安定ではダメなので、原子番号84以上の不安定な原子核は、放射線を出しながらより安定な原子核に変換するということをします。

そこで、そんな不安定な原子核の半数(半分)が崩壊するのにかかる時間のことを半減期と呼んでいます。

以上が半減期についての説明です。難しいことは1つもないと思います。

ここで覚えておいてほしいのが、「毎秒崩壊を起こす原子核の数は一定である」ということです。

例えば、2000個の不安定な原子核があるとします。この原子核は毎秒全体の1/10ずつ崩壊するという決まりがあるとします。(原子核によって違います)

すると、1秒後には2000×1/10=200個崩壊するので、崩壊せずに残っている原子核は1800個です。

2秒後には1800×1/10=180個が崩壊するので、崩壊せずに残っている原子核は1800-180=1620個・・・

という感じになります。崩壊の速度には決まりがあるということを覚えておいてください。

半減期のグラフ

ではここで、半減期についてのグラフを考えてみます。有名なグラフなのでぜひ学習してみてください。

今、半減期がTの原子核がN₀個あるとします。

この原子核は、時間が2T、3T・・・と経っていくと数はどのように変化していくのでしょうか？そのことをグラフにしてみます。

時間がT経つと、残存量が半分になるのは先ほど学習しました。

もともとN₀個あった原子核がT経つとN₀/2個になります。

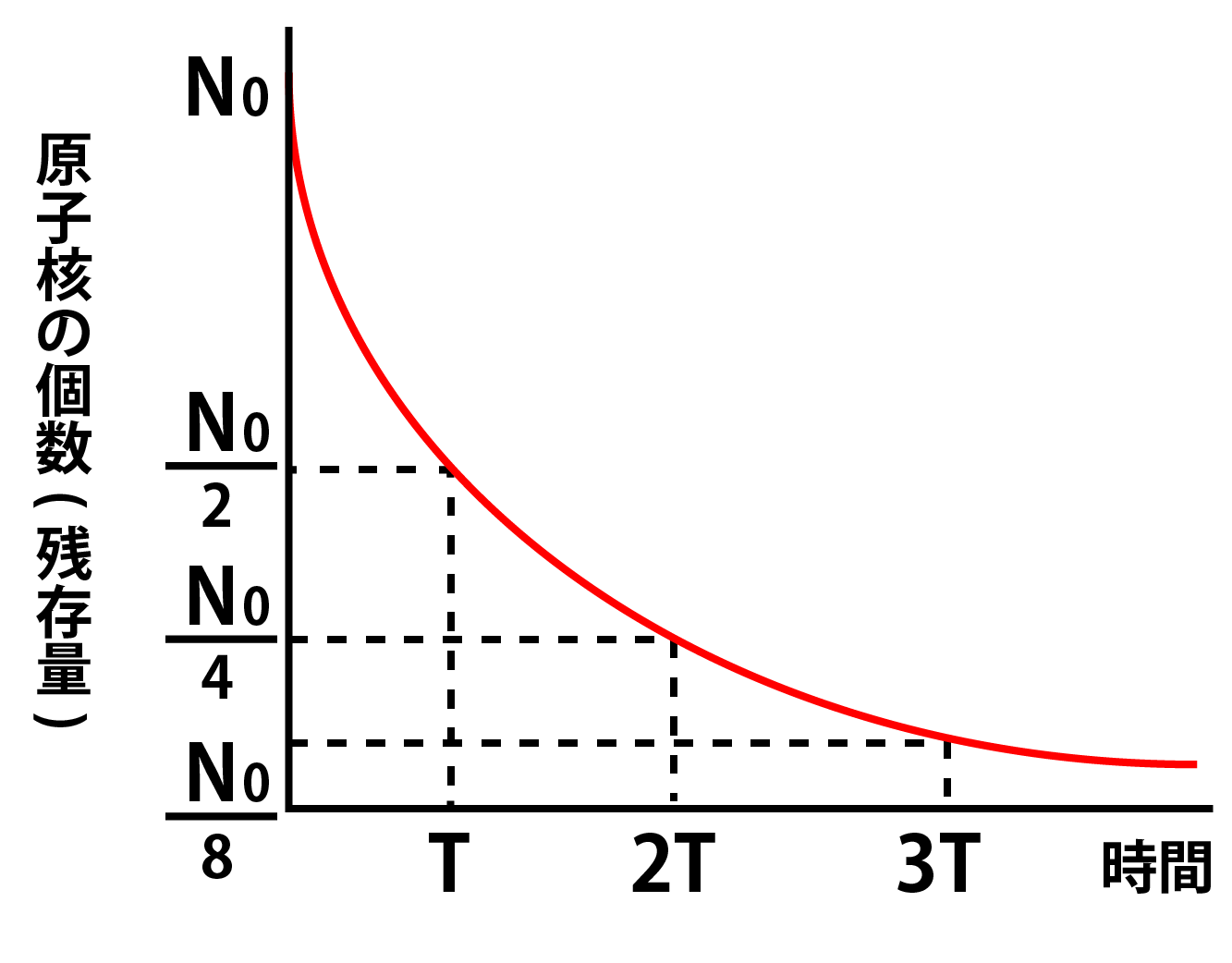
ここからさらにT経つとN₀/2×1/2=N₀/4になります。これの繰り返しです。このことをグラフにすると、以下のグラフになります。

[半減期のグラフ]

難しくはないと思います。この半減期のグラフはとても有名なので、ぜひ頭に入れておいてください。

２：半減期の計算方法

上記のグラフより、時間がTなら原子核の個数（残存量）はN₀/2、2Tなら(1/2)²N₀、3Tなら(1/2)³N₀・・・でした。

では、時間がtのときの残存量をNとすると、以下のような式が成り立ちますね。

[半減期の計算式]

※T：半減期、N₀：最初の量

この式（公式）は半減期の計算問題では必ず使うことになるので、必ず覚えておきましょう！次の章で、この半減期の計算式を使って問題を解いてみます。

３：半減期の計算問題

先ほど学習した半減期の計算公式を使って、半減期に関する問題を解いてみましょう！

[半減期の計算問題]
ラジウムの半減期は1600年である。次の問に答えよ。
(1)48gのラジウムがある。崩壊しないで残っているラジウムが6gになるのは何年後か。
(2)2gのラジウムは、800年後には何gになっているか。

[解答＆解説]

(1)

半減期の計算公式に値を入れていきましょう！

6=48×(1/2)^t/1600より、6/48=(1/2)^t/1600なので、

(1/2)³=(1/2)^t/1600

よって、3=t/1600

t=4800[年]・・・(答)

(2)

これも半減期の計算公式を使っていきます。

N

=2×(1/2)^800/1600

=2×(1/2)^1/2

=√2

=1.41[g]・・・(答)

半減期の計算公式を覚えていれば難しくないですよね？

半減期のまとめ

半減期について理解できましたでしょうか？

半減期とは、不安定な原子核の半数(半分)が崩壊するのにかかる時間のことでした。

特に、半減期の計算では、公式を必ず使うので、暗記しておきましょう！