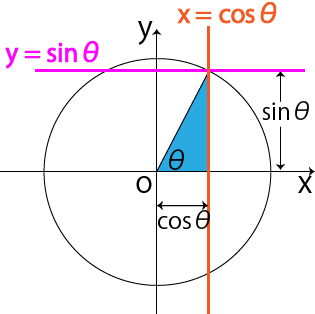
【三角関数の基礎】角度の求め方とは？（sinθ=1/2からθを計算）

三角関数の基礎では、角度を求めるということをよく行います。今回は、その角度の求め方についての記事です。

例えば、
 　

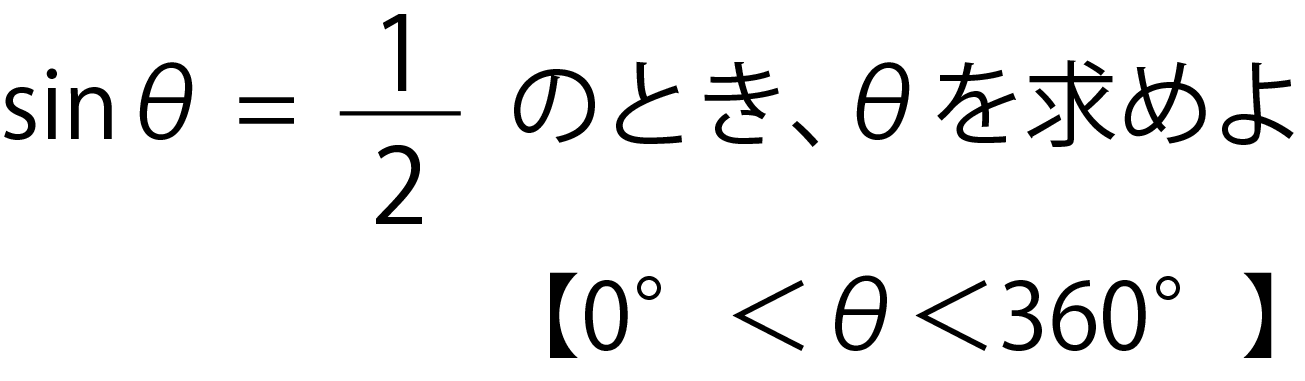
などといった問題があります。「代表的な角度（30°、45°、60°など）のsin , cos , tanの値は暗記してるよ」という人もいるかもしれませんが、それでは三角関数の基礎がわかっていない、それを忘れてしまうとなにもできないということになってしまいます…。

今回は、それを忘れても大丈夫なように、改めて単位円を使って、角度の求め方を解説していきます。

三角関数の基本的な理解に役立つ記事のまとめもぜひ参考にしてみてください！

【PR】勉強を効率的に継続して、志望校に合格したい方必見！

↓無料ダウンロードはこちら↓

１．知ってないとマズい！まずはこれを覚えよう！

上記の問題を単位円を使って考えていきます。まず、ここで覚えるべき事柄は次の２つです。
単位円上で、
sin はy座標を表し、cos はx座標を表す。

「sinはy , cosはx」と何度も唱えて覚えましょう♪

２．三角関数の角度の求め方

上記の問題を使って、具体的な手順を紹介します。下に図もあるので照らし合わせながら読むとわかりやすいですよ。

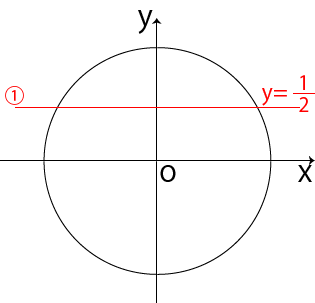
①：単位円上に、y = の直線を描く。
【今回はsinθ = でした。sinは単位円上ではyを表します。（１．知ってないとマズい！まずはこれを覚えよう！参照）】

②：①で描いた直線と単位円の交点を原点と結び、その交点から、x軸へ垂線を下す。

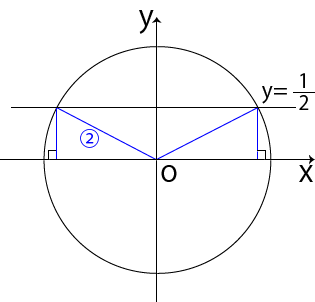
③：①と②からできあがった三角形に注目し、θの値を求める。

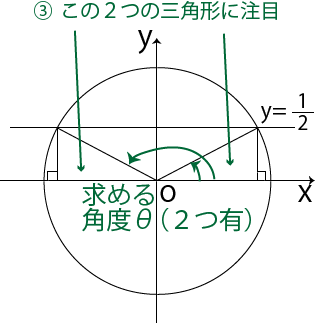
今回は、θの値も求めてみます。まずは２つの三角形の辺の比に注目しましょう。

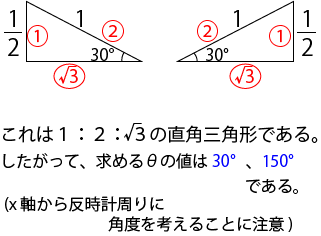
まとめ

最終段階で、角度を求めるときには、辺の比に注目しましょう。

最後に、必ず覚えておかなくてはならない、三角形の辺の比に関する図を載せておきます。

【参考】
三角関数に関する記事はまだまだたくさんあるのでぜひこれらも参考にしてみてください♪

「５分で分かる！正弦定理の公式・解き方」

「三角関数の基礎　試験にでる要点まとめ」

「三角関数の基礎　必ず覚えておかなくてはならない5つの性質」

「三角関数の基礎2　加法定理　公式・証明・覚え方」

「三角関数の基礎3　積和の公式&和積の公式」

「三角関数の基礎4　三角関数の合成のコツ」